题目内容
12.已知f(x)=1g$\frac{1+x}{1-x}$,x∈(-1,1),若f(a)=$\frac{1}{2}$,则 f(-a)=-$\frac{1}{2}$.分析 由已知条件利用函数的性质和对数的运算法则求解.
解答 解:∵f(x)=1g$\frac{1+x}{1-x}$,x∈(-1,1),f(a)=$\frac{1}{2}$,
∴f(a)=lg$\frac{1+a}{1-a}$=$\frac{1}{2}$,
∴f(-a)=lg$\frac{1-a}{1+a}$=-lg$\frac{1+a}{1-a}$=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质和对数运算法则的合理运用.

练习册系列答案
相关题目
20.已知△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则边BC上的中线长为( )
| A. | $\frac{\sqrt{21}}{2}$ | B. | $\frac{\sqrt{26}}{2}$ | C. | $\frac{\sqrt{29}}{2}$ | D. | $\frac{\sqrt{23}}{2}$ |
1.函数y=3x+$\sqrt{2x-1}$(x≥2)的值域是( )
| A. | [$\frac{4}{3},+∞$) | B. | [6+$\sqrt{3},+∞$) | C. | [6,+∞) | D. | [$\sqrt{3},+∞$) |
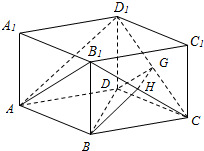 已知ABCD-A1B1C1D1 是直四棱拄,其底面是边长为m的菱形,∠BAD=60°,对角面 BDD1B1是矩形,G,H分别是CD1,B1C的中点.
已知ABCD-A1B1C1D1 是直四棱拄,其底面是边长为m的菱形,∠BAD=60°,对角面 BDD1B1是矩形,G,H分别是CD1,B1C的中点.