题目内容
12.已知函数f(x)=$\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}$.设△ABC的三个内角A,B,C的对边分别为a,b,c,且c=$\sqrt{7}$,f(C)=0.(1)求角C;
(2)若向量$\overrightarrow m=(1,sinA)$与向量$\overrightarrow n=(3,sinB)$共线,求a,b的值.
分析 (1)化简函数的表达式为一个角的一个三角函数的形式,然后利用f(C)=0,求出C.
(2)利用向量$\overrightarrow m=(1,sinA)$与向量$\overrightarrow n=(3,sinB)$共线,和余弦定理求出a,b的值.
解答 解:(1)$f(x)=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x-1=sin(2x-\frac{π}{6})-1$------3
∴$f(C)=sin(2C-\frac{π}{6})-1=0$即$sin(2C-\frac{π}{6})=1$------4
∵0<C<π,
∴$-\frac{π}{6}<2C-\frac{π}{6}<\frac{11π}{6}$,
∴$2C-\frac{π}{6}=\frac{π}{2}$------5
∴$C=\frac{π}{3}$------6
(2)∵$\overrightarrow m∥\overrightarrow n$,
∴sinB-3sinA=0------7
据正弦定理可得 b-3a=0…①------9
又由余弦定理可得 c2=a2+b2-2abcosC
而$c=\sqrt{7}$,$C=\frac{π}{3}$,∴7=a2+b2-ab…②------11
由①②知,a=1b=3------12
点评 本题是基础题,考查三角函数的化简求值,三角函数的周期的求法,余弦定理的应用,向量的应用,考查计算能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.(理) 曲线C:y=x3(x≥0)在点x=1处的切线为l,则由曲线C、直线l及x轴围成的封闭图形的面积是( )
| A. | 1 | B. | $\frac{1}{12}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
7.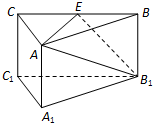 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |
17.已知f(x)是定义在[0,+∞)上的单调递增函数,则满足f (2x-1)<f($\frac{1}{3}$)的x的取值范围是( )
| A. | ( $\frac{1}{3}$,$\frac{2}{3}$ ) | B. | [$\frac{1}{3}$,$\frac{2}{3}$ ) | C. | [$\frac{1}{2}$,$\frac{2}{3}$ ) | D. | ( $\frac{1}{2}$,$\frac{2}{3}$ ) |
4.若不等式$\frac{1}{x}$<2和|x|>$\frac{1}{3}$同时成立,则x的取值范围是( )
| A. | -$\frac{1}{2}$<x<$\frac{1}{3}$ | B. | x>$\frac{1}{2}$或x<-$\frac{1}{3}$ | C. | x>$\frac{1}{2}$或x<$\frac{1}{3}$ | D. | x>$\frac{1}{2}$ |
1.已知下列各组命题,其中p是q的充分必要条件的是( )
| A. | p:m≤-2或m≥6;q:y=x2+mx+m+3有两个不同的零点 | |
| B. | p:$\frac{f(-x)}{f(x)}$=1;q:y=f(x)是偶函数 | |
| C. | p:cos α=cos β;q:tan α=tan β | |
| D. | p:A∩B=A;q:A⊆U,B⊆U,∁UB⊆∁UA |
2.已知-个三棱锥与一个四棱锥,它们的所有棱为1,将三棱锥与四棱锥的侧面粘在一起使之完全重合,则所得到的多面体是( )
| A. | 五面体 | B. | 六面体 | C. | 七面体 | D. | 八面体 |