题目内容
【题目】等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
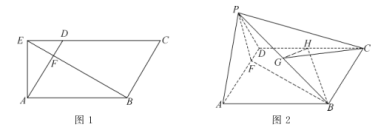
于![]() ,如图①.将
,如图①.将![]() 沿
沿![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,如图②.
,如图②.
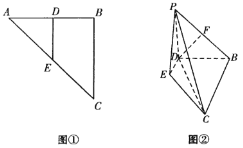
(Ⅰ)若![]() 为
为![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)先证![]() 平面
平面![]() 得
得![]() ,由
,由![]() 为
为![]() 的中点,
的中点,![]() ,得
,得![]() ,进而证明
,进而证明![]() 平面
平面![]() 即可证明;(Ⅱ)证明三棱锥
即可证明;(Ⅱ)证明三棱锥![]() 的体积最大时DB=2, 以
的体积最大时DB=2, 以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别求面
,分别求面![]() 和面PEB的法向量,由空间向量二面角公式求解即可
和面PEB的法向量,由空间向量二面角公式求解即可
(I)![]()
![]() ,
,![]() ,
,![]() ∩
∩![]() =D
=D
![]()
![]() 平面
平面![]() ,
,
又在图①中![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() 是
是![]() 的中点,
的中点,
![]()
![]()
![]()
![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
![]()
![]() .
.
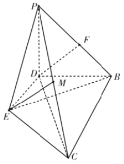
(Ⅱ)设![]() ,由
,由![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,
,
得三棱锥![]() 的体积最大时,
的体积最大时,![]() .
.
![]()
![]() ,
,
以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]()
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]()
则![]()
![]()
令![]() 则
则![]() ,
,![]() ,则
,则![]()
设面![]() 的法向量为
的法向量为![]()
则![]()
![]()
令![]() 则
则![]() ,
,![]() ,则
,则![]()
![]()
![]()
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】某企业生产一种产品,从流水线上随机抽取100件产品,统计其质量指标值并绘制频率分布直方图(如图):
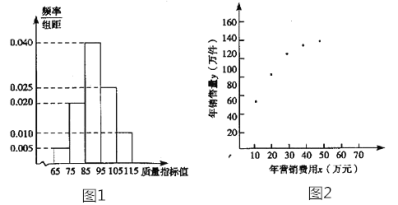
规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年年营销费用
(单位:万件)的影响,对近5年年营销费用![]() 和年销售量
和年销售量![]() 数据做了初步处理,得到如图的散点图及一些统计量的值.
数据做了初步处理,得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
⑦用所求的回归方程估计该企业应投人多少年营销费,才能使得该企业的年收益的预报值达到最大?(收益=销售利润营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() 其回归直线
其回归直线![]() 均斜率和截距的最小二乘估计分别为
均斜率和截距的最小二乘估计分别为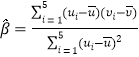 ,
,![]() .
.
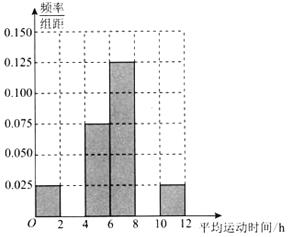
【题目】已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:h),汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:
平均运动时间 | 频数 | 频率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合计 | 300 | 1 |
(1)求抽取的女职工的人数;
(2)①根据频率分布表,求出m、n、p的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h的概率;
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下2×2列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |