题目内容
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和左视图在下面画出(单位:cm).
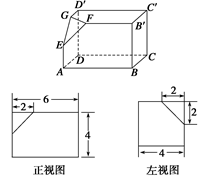
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥平面EFG.

(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥平面EFG.
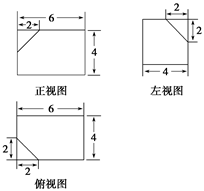
(1)
(2)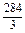 cm(3)证明略
cm(3)证明略

(2)
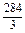 cm(3)证明略
cm(3)证明略 如图(1)所示.
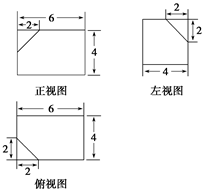
图(1)
(2)解 所求多面体体积
V=V长方体-V正三棱锥
=4×4×6-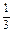 ×(
×(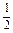 ×2×2)×2=
×2×2)×2=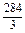 (cm3).
(cm3).
(3)证明 如图,在长方体ABCD—A′B′C′D′中,
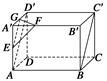
连接AD′,则AD′∥BC′.
因为E,G分别为AA′,A′D′的中点,
所以AD′∥EG,从而EG∥BC′.
又BC′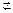 平面EFG,
平面EFG,
所以BC′∥面EFG.

图(1)
(2)解 所求多面体体积
V=V长方体-V正三棱锥
=4×4×6-
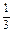 ×(
×(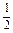 ×2×2)×2=
×2×2)×2=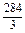 (cm3).
(cm3).(3)证明 如图,在长方体ABCD—A′B′C′D′中,

连接AD′,则AD′∥BC′.
因为E,G分别为AA′,A′D′的中点,
所以AD′∥EG,从而EG∥BC′.
又BC′
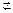 平面EFG,
平面EFG, 所以BC′∥面EFG.

练习册系列答案
相关题目
 α,b
α,b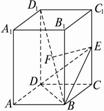
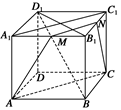
 中,
中,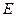 、
、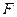 、
、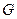 分别是棱
分别是棱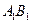 、
、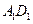 、
、 的中点.
的中点.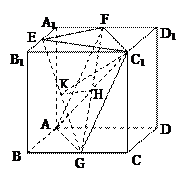
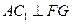 ;
; 到平面
到平面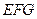 的距离;
的距离;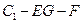 的大小.
的大小.