题目内容
如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.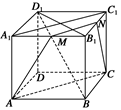
(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.

(1)不是异面直线(2)D1B与CC1是异面直线
(1)不是异面直线.理由如下:
∵M、N分别是A1B1、B1C1的中点.
∴MN∥A1C1,
又∵A1A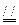 D1D,而D1D
D1D,而D1D 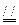 C1C,∴A1A C1C,∴四边形A1ACC1为平行四边形.
C1C,∴A1A C1C,∴四边形A1ACC1为平行四边形.
∴A1C1∥AC,得到MN∥AC,
∴A、M、N、C在同一个平面内,
故AM和CN不是异面直线.
(2)是异面直线,证明如下:
假设D1B与CC1在同一个平面D1CC1内,
则B∈平面CC1D1,C∈平面CC1D1.
∴BC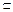 平面CC1D1,
平面CC1D1,
这与正方体ABCD—A1B1C1D1中BC⊥面CC1D1相矛盾.
∴假设不成立,故D1B与CC1是异面直线.
∵M、N分别是A1B1、B1C1的中点.
∴MN∥A1C1,
又∵A1A
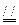 D1D,而D1D
D1D,而D1D 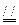 C1C,∴A1A C1C,∴四边形A1ACC1为平行四边形.
C1C,∴A1A C1C,∴四边形A1ACC1为平行四边形.∴A1C1∥AC,得到MN∥AC,
∴A、M、N、C在同一个平面内,
故AM和CN不是异面直线.
(2)是异面直线,证明如下:
假设D1B与CC1在同一个平面D1CC1内,
则B∈平面CC1D1,C∈平面CC1D1.
∴BC
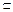 平面CC1D1,
平面CC1D1,这与正方体ABCD—A1B1C1D1中BC⊥面CC1D1相矛盾.
∴假设不成立,故D1B与CC1是异面直线.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
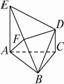
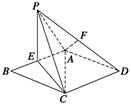 (1)试确定E点位置;
(1)试确定E点位置;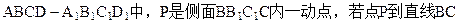 与直线
与直线