题目内容
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
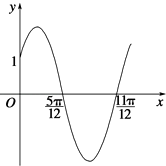
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
【答案】①③
【解析】解:①由正切函数的图象可知函数y=tanx在第一象限是增函数,命题正确;
②f(x)=cos2( ![]() ﹣x)=cos(
﹣x)=cos( ![]() ﹣2x)=sin2x,f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),故命题不正确;
﹣2x)=sin2x,f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),故命题不正确;
③∵0=4sin(2× ![]() ﹣
﹣ ![]() ),∴命题正确;
),∴命题正确;
④由2k ![]() ≤x+
≤x+ ![]() ≤2k
≤2k ![]() 可解得函数y=sin(x+
可解得函数y=sin(x+ ![]() )的单调递增区间为[2k
)的单调递增区间为[2k ![]() ,2k
,2k ![]() ]k∈Z,故命题不正确.
]k∈Z,故命题不正确.
综上,所有正确的命题的题号:①③,
故答案为:①③
①由正切函数的图象可知命题正确;
②化简可得f(x)=sin2x,由f(﹣x)=sin(﹣2x)=﹣sin2x=﹣f(x),可知命题不正确;
③代入有0=4sin(2× ![]() ﹣
﹣ ![]() ),可得命题正确;
),可得命题正确;
④由2k ![]() ≤x+
≤x+ ![]() ≤2k
≤2k ![]() 可解得函数y=sin(x+
可解得函数y=sin(x+ ![]() )的单调递增区间为[2k
)的单调递增区间为[2k ![]() ,2k
,2k ![]() ]k∈Z,比较即可得命题不正确.
]k∈Z,比较即可得命题不正确.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目