题目内容
已知关于x的不等式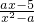 <0的解集为M.
<0的解集为M.
(1)当a=4时,求集合M;
(2)若3∈M且5∉M,求实数a的取值范围.
解:(1)a=4时,不等式化为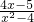 <0,即(4x-5)(x2-4)<0
<0,即(4x-5)(x2-4)<0
利用穿根法解得M=(-∞,-2)∪( ,2).
,2).
(2)当a≠25时,由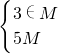 得
得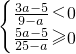
∴a∈[1, )∪(9,25);
)∪(9,25);
当a=25时,不等式为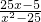 <0?M=(-∞,-5)∪(
<0?M=(-∞,-5)∪( ,5).
,5).
满足3∈M且5∉M,∴a=25满足条件.
综上所述,得a的取值范围是[1, )∪(9,25].
)∪(9,25].
分析:(1)当a=4时,不等式化为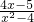 <0,推出同解不等式,利用穿根法解不等式求得集合M;
<0,推出同解不等式,利用穿根法解不等式求得集合M;
(2)对a=25,和a≠25时分类讨论,用3∈M且5∉M,推出不等式组,然后解分式不等式组,求实数a的取值范围.
点评:本题考查其他不等式的解法,元素与集合关系的判断,考查穿根法,分式不等式的解法,是中档题.
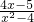 <0,即(4x-5)(x2-4)<0
<0,即(4x-5)(x2-4)<0利用穿根法解得M=(-∞,-2)∪(
 ,2).
,2).(2)当a≠25时,由
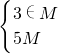 得
得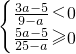
∴a∈[1,
 )∪(9,25);
)∪(9,25);当a=25时,不等式为
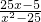 <0?M=(-∞,-5)∪(
<0?M=(-∞,-5)∪( ,5).
,5).满足3∈M且5∉M,∴a=25满足条件.
综上所述,得a的取值范围是[1,
 )∪(9,25].
)∪(9,25].分析:(1)当a=4时,不等式化为
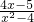 <0,推出同解不等式,利用穿根法解不等式求得集合M;
<0,推出同解不等式,利用穿根法解不等式求得集合M;(2)对a=25,和a≠25时分类讨论,用3∈M且5∉M,推出不等式组,然后解分式不等式组,求实数a的取值范围.
点评:本题考查其他不等式的解法,元素与集合关系的判断,考查穿根法,分式不等式的解法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.