题目内容
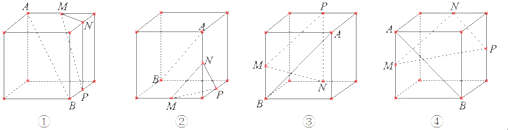
下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出△MNP为直角三角形的图形的序号是 ．
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：根据正方体的几何性质，设棱长为2，运用线面垂直的性质，勾股定理判断
解答：
解：①∵NP⊥面AMN，MN?面AMN，
∴NP⊥MN，
∴△MNP为直角三角形
②根据正方体的几何性质得出△MNP为正三角形，
③设棱长为2，
根据正方体的边长得出MP=MN=
，NP=2，
故∴△MNP不是直角三角形，
④设棱长为2，根据正方体的结合性质得：MN=
，NP=
，MP=2
，
根据勾股定理可判断△MNP为直角三角形
故答案为：①④
∴NP⊥MN，
∴△MNP为直角三角形
②根据正方体的几何性质得出△MNP为正三角形，
③设棱长为2，
根据正方体的边长得出MP=MN=
| 6 |
故∴△MNP不是直角三角形，
④设棱长为2，根据正方体的结合性质得：MN=
| 6 |
| 2 |
| 2 |
根据勾股定理可判断△MNP为直角三角形
故答案为：①④
点评：本题考查了正方体的性质，运用判断线线垂直问题，属于中档题，关键是求准线段长度．
练习册系列答案
相关题目
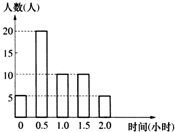某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果用下面的条形图表示．根据条形图可得这50名学生这一天平均的课外阅读时间为