题目内容
18.为了美化校园环境,某校计划对学生乱扔垃圾现象进行罚款处理,为了更好的了解学生的态度,随机抽取了200人进行了调查,得到如下数据:| 罚款金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 会继续乱扔垃圾的人数y | 80 | 50 | 40 | 20 | 10 |
(Ⅱ)若以调查数据为基础,从这5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
分析 (I)利用最小二乘法,分别计算两组数据的平均数,代入a=$\overline{y}$-b$\overline{x}$,求出a值,可得回归方程,进而可分析罚款金额的预报值.
(Ⅱ)确定从5种金额中随机抽取2种,可得总的抽选方法,满足金额之和不低于25元的有4种,即可求得概率;
解答 解:(Ⅰ)∵$\overline{x}$=$\frac{1}{5}$(0+5+10+15+20)=10,$\overline{y}$=$\frac{1}{5}$(80+50+40+20+10)=40,
∴a=$\overline{y}$-b$\overline{x}$=40+3.4×10=74,
∴$\hat{y}=-3.4x+74$,
要使乱扔垃圾者不超过20%,则$\hat{y}≤40$,
解得:x≥10,
即要使乱扔垃圾者不超过20%,罚款金额至少是10元;
(Ⅱ)设“两种金额之和不低于25元”的事件为A,从5种金额中随机抽取2种,总的抽选方法共有${C}_{5}^{2}$=10种,
满足金额之和不低于25元的有4种,故所求概率为P(A)=$\frac{4}{10}$=$\frac{2}{5}$.
点评 本题考查概率的计算,考查回归直线的求法,考查学生的计算能力,属于中档题

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}(a-3)x+5,(x≤1)\\ \frac{2a}{x},(x>1)\end{array}\right.$,满足对任意的,都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0成立,则a的取值范围是( )
| A. | (0,3) | B. | (0,3] | C. | (0,2) | D. | (0,2] |
9.在△ABC中角A,B,C所对的边分别为a,b,c,若a=2,b=2$\sqrt{3}$,A=30°,则B=( )
| A. | 60°或120° | B. | 60° | C. | 120° | D. | 30° |
13.在△ABC中,角A,B,C的对边分别是a,b,c,若b=asinB,则A等于( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
8.设偶函数f(x)的定义域为R,f(2)=-3,对于任意的x≥0,都有f′(x)>2x,则不等式f(x)≤x2-7的解集为( )
| A. | (-2,+∞) | B. | (-2,2) | C. | (-∞,-2) | D. | (+∞,+∞) |
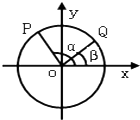 如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.
如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.