题目内容
(本题满分14分)已知函数![]()
![]() 。
。
(Ⅰ)若函数![]() 在
在![]() 上为增函数,求正实数
上为增函数,求正实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,求
时,求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)当![]() 时,求证:对大于
时,求证:对大于![]() 的任意正整数
的任意正整数![]() ,都有
,都有![]() 。
。
解:(I)![]() ……………1分
……………1分
∵ 函数![]() 在
在![]() 上为增函数
上为增函数
∴ ![]() 对
对![]() 恒成立, ……………………2分
恒成立, ……………………2分
∴ ![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立
恒成立
∴ ![]() ……………………4分
……………………4分
(II)当![]() 时,
时,![]() ,
,
∴ 当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增, ………………6分
上单调递增, ………………6分
∴ ![]() 在区间
在区间![]() 上有唯一极小值点,故
上有唯一极小值点,故![]() ……7分
……7分
又 ![]()
∵ ![]() ∴
∴ ![]()
∴ ![]() 在区间
在区间![]() 上的最大值
上的最大值![]()
综上可知,函数![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() 。………………9分
。………………9分
(Ⅲ)当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为增函数。
上为增函数。
当![]() 时,令
时,令![]() ,则
,则![]() ,故
,故![]() ……………………11分
……………………11分
∴ 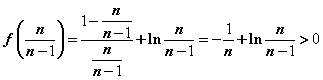 即
即![]() ………12分
………12分
∴ ![]()
∴![]() …………………13分
…………………13分
∴ ![]()
即对大于![]() 的任意正整数
的任意正整数![]() ,都有
,都有![]() ……………………14分
……………………14分

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
