题目内容
5.已知实数x,y满足$\left\{\begin{array}{l}{y≥{x}^{2}}\\{x-y+2≥0}\end{array}\right.$,则z=x+y的取值范围是( )| A. | (0,6) | B. | [-$\frac{1}{4}$,6] | C. | [-$\frac{1}{4}$,0] | D. | [$\frac{3}{4}$,6] |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,通过平移从而求出z的取值范围.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
由z=x+y得y=-x+z,即直线的截距最大,z也最大.
平移直线y=-x+z,即直线y=-x+z经过点A时,截距最大,此时z最大,
由$\left\{\begin{array}{l}{y={x}^{2}}\\{x-y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,即A(2,4),
则z=2+4=6.
当直线y=-x+z与y=x2相切时,直线的截距最小,此时z最小,
函数y=x2的导数f′(x)=2x,
由2x=-1,解得x=$-\frac{1}{2}$,此时y=$\frac{1}{4}$,即切点坐标为($-\frac{1}{2}$,$\frac{1}{4}$),
则z=$-\frac{1}{2}$+$\frac{1}{4}$=-$\frac{1}{4}$,
∴-$\frac{1}{4}$≤z≤6,
故z的取值范围是[-$\frac{1}{4}$,6],
故选:B.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义以及直线和抛物线的相切,结合数形结合的数学思想是解决此类问题的基本方法.综合性较强,涉及的知识点较多.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
15. 图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
 图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
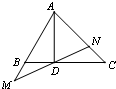 如图,在△ABC中,$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N.若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+2μ的最小值是$\frac{8}{3}$.
如图,在△ABC中,$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N.若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+2μ的最小值是$\frac{8}{3}$.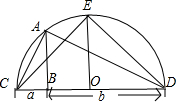 “无字证明”(proofs without words)就是将数学命题用简单、有创意而且易于理解的几何图形来呈现,请利用下面两个三角形(△ACD和△ECD)的面积关系,写出高中数学中的一个重要关系式:$\sqrt{ab}≤\frac{1}{2}(a+b)$.
“无字证明”(proofs without words)就是将数学命题用简单、有创意而且易于理解的几何图形来呈现,请利用下面两个三角形(△ACD和△ECD)的面积关系,写出高中数学中的一个重要关系式:$\sqrt{ab}≤\frac{1}{2}(a+b)$.