题目内容
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知该四棱锥底面边长是2m,高是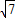 m,
m,(1)求侧棱与底面所成角;
(2)求制造这个塔顶需要多少铁板?
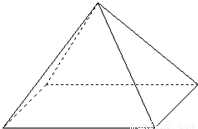
【答案】分析:(1)正四棱锥S-ABCD中,连结AC和BD交于O,连接SO.可得SO⊥ABCD,∠SAO就是侧棱SA与底面ABCD内的所成角.
Rt△SOA中利用三角函数的定义,结合题中数据算出tan∠SAO=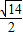 ,即得侧棱与底面所成角等于arctan
,即得侧棱与底面所成角等于arctan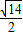 ;
;
(2)作SP⊥AB于P,连接OP.Rt△SOP中,算出SP=2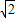 (m),可得△SAB的面积S=2
(m),可得△SAB的面积S=2 (m2).由此即可得到正四棱锥的侧面积,从而得到制造这个塔顶需要铁板的面积.
(m2).由此即可得到正四棱锥的侧面积,从而得到制造这个塔顶需要铁板的面积.
解答:解:(1)如图所示,设正四棱锥S-ABCD中,连结AC和BD交于O,连接SO.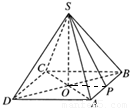
∵SO⊥ABCD,可得OA是侧棱SA在底面ABCD内的射影
∴∠SAO就是侧棱SA与底面ABCD内的所成角
Rt△SOA中,SO=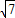 m,AO=
m,AO=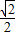 AB=
AB=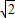 m
m
∴tan∠SAO=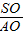 =
=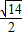
因此,∠SAO=arctan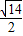 ,即侧棱与底面所成角等于arctan
,即侧棱与底面所成角等于arctan ;
;
(2)作SP⊥AB于P,连接OP.
∵在Rt△SOP中,SO=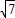 (m),OP=
(m),OP= BC=1(m),
BC=1(m),
∴SP=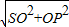 =2
=2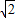 (m),
(m),
则△SAB的面积S= ×AB×SP=
×AB×SP= ×2×2
×2×2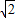 =2
=2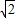 (m2).
(m2).
∴四棱锥的侧面积是4×2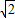 =8
=8 (m2),
(m2),
即制造这个塔顶需要8 m2铁板.
m2铁板.
点评:本题给出正四棱锥,求侧棱与底面所成角,并求制造这个塔顶需要铁板的面积.着重考查了正四棱锥的定义与性质、直线与平面所成角的求法等知识,属于中档题.
Rt△SOA中利用三角函数的定义,结合题中数据算出tan∠SAO=
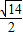 ,即得侧棱与底面所成角等于arctan
,即得侧棱与底面所成角等于arctan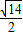 ;
;(2)作SP⊥AB于P,连接OP.Rt△SOP中,算出SP=2
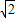 (m),可得△SAB的面积S=2
(m),可得△SAB的面积S=2 (m2).由此即可得到正四棱锥的侧面积,从而得到制造这个塔顶需要铁板的面积.
(m2).由此即可得到正四棱锥的侧面积,从而得到制造这个塔顶需要铁板的面积.解答:解:(1)如图所示,设正四棱锥S-ABCD中,连结AC和BD交于O,连接SO.

∵SO⊥ABCD,可得OA是侧棱SA在底面ABCD内的射影
∴∠SAO就是侧棱SA与底面ABCD内的所成角
Rt△SOA中,SO=
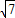 m,AO=
m,AO=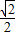 AB=
AB=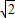 m
m∴tan∠SAO=
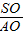 =
=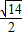
因此,∠SAO=arctan
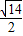 ,即侧棱与底面所成角等于arctan
,即侧棱与底面所成角等于arctan ;
;(2)作SP⊥AB于P,连接OP.
∵在Rt△SOP中,SO=
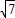 (m),OP=
(m),OP= BC=1(m),
BC=1(m),∴SP=
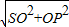 =2
=2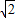 (m),
(m),则△SAB的面积S=
 ×AB×SP=
×AB×SP= ×2×2
×2×2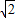 =2
=2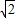 (m2).
(m2).∴四棱锥的侧面积是4×2
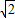 =8
=8 (m2),
(m2),即制造这个塔顶需要8
 m2铁板.
m2铁板.点评:本题给出正四棱锥,求侧棱与底面所成角,并求制造这个塔顶需要铁板的面积.着重考查了正四棱锥的定义与性质、直线与平面所成角的求法等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知该四棱锥底面边长是2m,高是
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知该四棱锥底面边长是2m,高是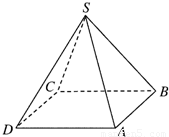 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为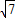 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?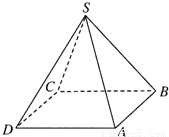 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?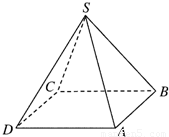 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?