题目内容
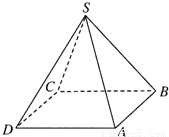 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?
【答案】分析:连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.在Rt△SOP中,SO=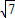 (m),OP=
(m),OP= BC=1,所以SP=2
BC=1,所以SP=2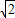 ,由此能求出制造这个塔顶需要多少铁板.
,由此能求出制造这个塔顶需要多少铁板.
解答: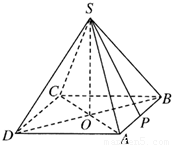 解:如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.
解:如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.
在Rt△SOP中,SO=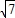 (m),OP=
(m),OP= BC=1(m),
BC=1(m),
所以SP=2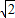 (m),
(m),
则△SAB的面积是 ×2×2
×2×2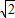 =2
=2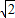 (m2).
(m2).
所以四棱锥的侧面积是4×2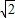 =8
=8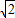 (m2),
(m2),
即制造这个塔顶需要8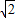 m2铁板.
m2铁板.
点评:本题考查四棱锥的侧面积的应用,解题时要认真审题,仔细解答,注意空间思维能力和空间想象能力的培养.
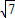 (m),OP=
(m),OP= BC=1,所以SP=2
BC=1,所以SP=2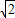 ,由此能求出制造这个塔顶需要多少铁板.
,由此能求出制造这个塔顶需要多少铁板.解答:
 解:如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.
解:如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.在Rt△SOP中,SO=
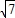 (m),OP=
(m),OP= BC=1(m),
BC=1(m),所以SP=2
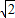 (m),
(m),则△SAB的面积是
 ×2×2
×2×2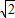 =2
=2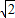 (m2).
(m2).所以四棱锥的侧面积是4×2
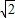 =8
=8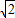 (m2),
(m2),即制造这个塔顶需要8
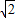 m2铁板.
m2铁板.点评:本题考查四棱锥的侧面积的应用,解题时要认真审题,仔细解答,注意空间思维能力和空间想象能力的培养.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知该四棱锥底面边长是2m,高是
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知该四棱锥底面边长是2m,高是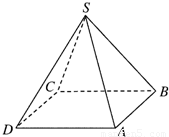 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?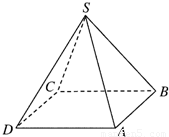 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?