题目内容
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是
,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是![]() 的中点,点E,F分别落在线段
的中点,点E,F分别落在线段![]() 上.已知
上.已知![]() ,记
,记![]() .
.

(1)试将污水管道的长度表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)已知![]() ,求此时管道的长度l;
,求此时管道的长度l;
(3)当![]() 取何值时,铺设管道的成本最低?并求出此时管道的长度.
取何值时,铺设管道的成本最低?并求出此时管道的长度.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,l取到最小值
时,l取到最小值![]()
【解析】
(1)由∠BHE=θ,H是AB的中点,易得![]() ,
,![]() ,
,![]() ,由污水净化管道的长度L=EH+FH+EF,则易将污水净化管道的长度L表示为θ的函数.
,由污水净化管道的长度L=EH+FH+EF,则易将污水净化管道的长度L表示为θ的函数.
(2)若![]() ,结合(1)中所得的函数解析式,代入易得管道的长度L的值.
,结合(1)中所得的函数解析式,代入易得管道的长度L的值.
(3)设sinθ+cosθ=t得![]() ,利用角的范围结合三角函数性质求得t的范围,再利用
,利用角的范围结合三角函数性质求得t的范围,再利用![]() 的单调性求最值即可
的单调性求最值即可
(1)由题![]() ,
,![]() ,
,
由于![]() ,
,![]() ,
,![]()
![]() ,
,![]()
(2)当![]() 时,
时,![]() ,
,
![]() ;
;
(3)![]()
设sinθ+cosθ=t则![]()
由于![]() ,所以
,所以
因为![]() 在
在 内单调递减,于是当
内单调递减,于是当![]() 时
时![]() .L的最小值
.L的最小值![]() 米.
米.
答:当![]() 时,所铺设管道的成本最低,此时管道的长度为
时,所铺设管道的成本最低,此时管道的长度为![]() 米
米

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限![]() 与所支出的总费用
与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1) 在给出的坐标系中作出散点图;
(2)求线性回归方程![]() 中的
中的![]() 、
、![]() ;
;
(3)估计使用年限为![]() 年时,车的使用总费用是多少?
年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式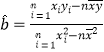 ,
, ![]() .)
.)



