题目内容
定义域为R的偶函数y=f(x)满足f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,则直线x=0,x=3,y=0与曲线y=f(x)所围成的封闭图形的面积为
2
令x=-1,由题意得f(-1+2)=f(-1)-f(1)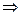 f(1)=f(-1)-f(1)
f(1)=f(-1)-f(1)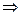 f(1)=f(-1)=0
f(1)=f(-1)=0
∴f(x+2)=f(x)即y=f(x)既是定义R上的偶函数,又是以2为周期的周期函数

如图为y=f(x)在[0,3]上的像
∴直线x=0,x=3,y=0与曲线y=f(x)所围成的封闭图形的面积为
S=-3
=-3×(-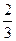 x3+6x2-18x)
x3+6x2-18x)
=-3[ (-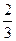 ×33+6×32-18×3)-(-
×33+6×32-18×3)-(-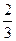 ×23+6×22-18×2)]
×23+6×22-18×2)]
=-3(-18+ +12)=2
+12)=2
 f(1)=f(-1)-f(1)
f(1)=f(-1)-f(1) f(1)=f(-1)=0
f(1)=f(-1)=0∴f(x+2)=f(x)即y=f(x)既是定义R上的偶函数,又是以2为周期的周期函数

如图为y=f(x)在[0,3]上的像
∴直线x=0,x=3,y=0与曲线y=f(x)所围成的封闭图形的面积为
S=-3

=-3×(-
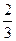 x3+6x2-18x)
x3+6x2-18x)
=-3[ (-
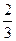 ×33+6×32-18×3)-(-
×33+6×32-18×3)-(-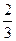 ×23+6×22-18×2)]
×23+6×22-18×2)]=-3(-18+
 +12)=2
+12)=2
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则函数
,则函数 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )



 ,则
,则 等于( )
等于( )
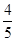

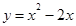 与直线
与直线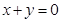 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )



 与直线
与直线 围成的封闭区域为M,则区域M的面积为( )
围成的封闭区域为M,则区域M的面积为( )

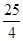
 与直线
与直线 及y=0所围成的图形的面积 .
及y=0所围成的图形的面积 .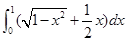 = .
= . ( )
( )