题目内容
设函数F（x）=sinx-xcosx，则判定F（x）的奇偶性的结果为：F（x）是
奇函数
奇函数
．分析：根据函数的定义域为R，且F（-x）=-F（x），可得F（x）是奇函数．
解答：解：由于函数F（x）=sinx-xcosx的定义域为R，F（-x）=sin（-x）+xcos（-x）=-sinx+xcosx=-F（x），
故F（x）是奇函数，
故答案为：奇函数．
故F（x）是奇函数，
故答案为：奇函数．
点评：本题主要考查判断函数的奇偶性的方法，属于基础题．
练习册系列答案
相关题目
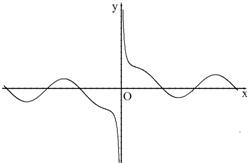如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=| 1 |
| x |
A、
| ||
| B、f（x）g（x） | ||
| C、f（x）-g（x） | ||
| D、f（x）+g（x） |
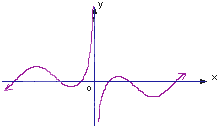设函数f（x）=sinx，g（x）=