题目内容
设函数f(x)=sinx-cosx+ax+1.
(1)当a=1,x∈[0,2π]时,求函数f(x)的单调区间与极值;
(2)若函数f(x)为单调函数,求实数a的取值范围.
(1)当a=1,x∈[0,2π]时,求函数f(x)的单调区间与极值;
(2)若函数f(x)为单调函数,求实数a的取值范围.
分析:(1)对函数f(x)=sinx-cosx+x+1求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值;
(2)由于函数f(x)为单调函数,则f′(x)≥0恒成立或f′(x)≤0恒成立,解出a即可.
(2)由于函数f(x)为单调函数,则f′(x)≥0恒成立或f′(x)≤0恒成立,解出a即可.
解答:解:(1)由f(x)=sinx-cosx+x+1=
sin(x-
)+x+1,0<x<2π,
知f′(x)=1+
sin(x+
).
令f′(x)=0,从而可得sin(x+
)=-
,
解得x=π,或x=
,
当x变化时,f′(x),f(x)变化情况如下表:
因此,由上表知f(x)的单调递增区间是(0,π)与(
,2π),单调递减区间是(π,
),
故函数f(x)的极小值为f(
)=
,极大值为f(π)=π+2;
(2)f′(x)=
sin(x+
)+a
由于函数f(x)为单调函数,
则f′(x)≥0恒成立或f′(x)≤0恒成立
∴
sin(x+
)+a≥0或
sin(x+
)+a≤0,
解得a≤-
或a≥
故实数a的取值范围为(-∞,-
]∪[
,+∞).
| 2 |
| π |
| 4 |
知f′(x)=1+
| 2 |
| π |
| 4 |
令f′(x)=0,从而可得sin(x+
| π |
| 4 |
| ||
| 2 |
解得x=π,或x=
| 3π |
| 2 |
当x变化时,f′(x),f(x)变化情况如下表:
| x | (0,π) | π | (π,
|
|
|||||
| f′(x) | + | 0 | - | 0 | + | ||||
| f(x) | 单调递增↑ | π+2 | 单调递减↓ |
|
单调递增↑ |
| 3π |
| 2 |
| 3π |
| 2 |
故函数f(x)的极小值为f(
| 3π |
| 2 |
| 3π |
| 2 |
(2)f′(x)=
| 2 |
| π |
| 4 |
由于函数f(x)为单调函数,
则f′(x)≥0恒成立或f′(x)≤0恒成立
∴
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
解得a≤-
| 2 |
| 2 |
故实数a的取值范围为(-∞,-
| 2 |
| 2 |
点评:本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合应用数学知识解决问题的能力.对于函数解答题,一般情况下都是利用导数来研究单调性或极值,利用导数为0得可能的极值点,通过列表得每个区间导数的正负判断函数的单调性,进而得出极值点.

练习册系列答案
相关题目
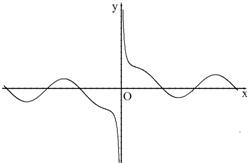 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=| 1 |
| x |
A、
| ||
| B、f(x)g(x) | ||
| C、f(x)-g(x) | ||
| D、f(x)+g(x) |
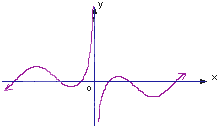 设函数f(x)=sinx,g(x)=
设函数f(x)=sinx,g(x)=