题目内容
(本题16分)已知函数 在定义域
在定义域 上是奇函数,(其中
上是奇函数,(其中 且
且 ).
).
(1)求出 的值,并求出定义域
的值,并求出定义域 ;
;
(2)判断 在
在 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(3)当 时,
时, 的值域范围恰为
的值域范围恰为 ,求
,求 及
及 的值.
的值.
【答案】
解:(1)由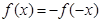 ,可得
,可得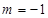
所以 ,
,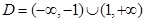
(2)当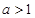 时,
时,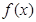 是减函数;
是减函数;
当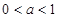 时,
时,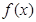 是增函数;
是增函数;
用定义证明(略)
(3)因为xÎ(r, a–2),定义域D=(–∞, –1)∪(1,+∞),
1o当r≥1时,则1≤r<a–2,即a>3,
所以f(x)在(r, a–2)上为减函数,值域恰为(1, +∞),所以f(a–2)=1,
即loga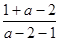 =loga
=loga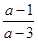 =1,即
=1,即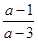 =a,
=a,
所以a=2+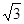 且r=1
且r=1
2o当r<1时,则(r, a–2) 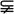 (–∞, –1),所以0<a<1
(–∞, –1),所以0<a<1
因为f(x)在(r, a–2)上为减函数,所以f(r)=1,a–2= –1,a=1(舍)
【解析】略

练习册系列答案
相关题目
 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合). ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明; (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.