题目内容
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
(1)求实数m的值,并写出区间D;
(2)若底数 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.
【答案】
解 (1) ∵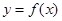 是奇函数,
是奇函数,
∴对任意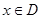 ,有
,有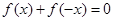 ,即
,即 .
.
化简此式,得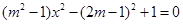 .恒成立,必有
.恒成立,必有
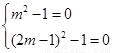 ,解得
,解得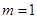 .
.
∴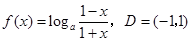 .
.
(2) 当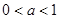 时,函数
时,函数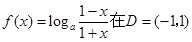 上是单调增函数.
上是单调增函数.
理由:令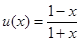 设
设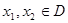 且
且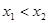 ,则:
,则:
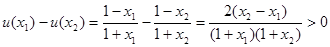
∴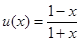 在
在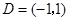 上单调递减,
上单调递减,
于是,当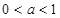 时,函数
时,函数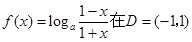 上是单调增函数.
上是单调增函数.
(3) ∵ 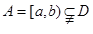 , ∴
, ∴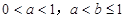 .
.
∴依据(2),当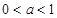 时,函数
时,函数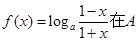 上是增函数,
上是增函数,
即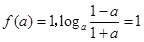 ,解得
,解得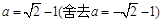 .
. 
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的