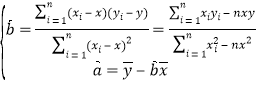题目内容
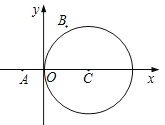
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
,![]() .
.
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
【答案】(1)![]() 或
或![]() .(2)
.(2)![]() .
.
【解析】
试题分析:(1)本题实质为直线被圆截得弦长问题,一般方法为利用垂径定理进行转化解决:先根据AB斜率得直线斜率![]() ,设直线方程
,设直线方程![]() ,再根据AB长得弦长
,再根据AB长得弦长![]() ,最后根据垂径定理得
,最后根据垂径定理得![]() ,根据圆心
,根据圆心![]() 到直线
到直线![]() 的距离公式得
的距离公式得![]() 代入得
代入得![]() ,解得
,解得![]() 或
或![]() ,(2)
,(2)![]() 点既在圆
点既在圆![]() 上,又满足
上,又满足![]() ,因此研究点
,因此研究点![]() 的个数,实质研究两曲线位置关系,先确定满足
的个数,实质研究两曲线位置关系,先确定满足![]() 的轨迹方程 ,利用直接法得
的轨迹方程 ,利用直接法得![]() ,也为圆,所以根据两圆位置关系可得点
,也为圆,所以根据两圆位置关系可得点![]() 的个数
的个数
试题解析:(1)圆![]() 的标准方程为
的标准方程为![]() ,所以圆心
,所以圆心![]() ,半径为
,半径为![]() .
.
因为![]() ,
,![]() ,
,![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,
,
设直线![]() 的方程为
的方程为![]() , ……………………………………………2分
, ……………………………………………2分
则圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() .…………………………4分
.…………………………4分
因为![]() ,
,
而![]() ,所以
,所以![]() , ……………………………6分
, ……………………………6分
解得![]() 或
或![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() .…………………………………8分
.…………………………………8分
(2)假设圆![]() 上存在点
上存在点![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
即![]() ,即
,即![]() , ………………………………10分
, ………………………………10分
因为![]() ,……………………………………12分
,……………………………………12分
所以圆![]() 与圆
与圆![]() 相交,
相交,
所以点![]() 的个数为
的个数为![]() .…………………………………………………………14分
.…………………………………………………………14分

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: