题目内容
【题目】设集合 A={x|2<x<4},B={a<x<3a}.
(1)若A∩B≠,求实数a的范围.
(2)若A∪B={x|2<x<6},求实数a的值.
【答案】
(1)解:∵集合 A={x|2<x<4},B={a<x<3a},
A∩B≠,
∴  或
或 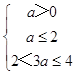 或
或 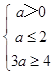 ,
,
解得 ![]() ≤a<4.
≤a<4.
∴实数a的范围是[ ![]() ,4)
,4)
(2)解:∵集合 A={x|2<x<4},B={a<x<3a},
A∪B={x|2<x<6},
∴ ![]() ,
,
解得a=2
【解析】(1)由A∩B≠,列出不等式组,能求出实数a的范围.(2)由A∪B={x|2<x<6},列出不等式组,能求出a.
【考点精析】解答此题的关键在于理解集合的并集运算的相关知识,掌握并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立.
B,反之也成立.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】某市为了普及法律知识,增强市民的法制观念,针对本市特定人群举办网上学法普法考试.为了解参考人群的法律知识水平,从一次普法考试中随机抽取了50份答卷进行分析,得到这50份答卷成绩的统计数据如下:
成绩分组 |
|
|
|
|
|
|
频数 | 2 | 5 | 12 | 16 | 10 | 5 |
(1)在答题卡的图中作出样本数据的频率分布直方图;
(2)试根据统计数据,估计本次普法考试的平均成绩![]() 和中位数( 同一组中的数据用该组区间的中点值作代表);
和中位数( 同一组中的数据用该组区间的中点值作代表);
(3)已知该市有100 万人参加考试,得分低于60 分的需要重考(不低于60 分为合格,不再重考).若每次重考的合格率都比上一次考试低6 个百分点,试估计第3 次重考的人数.
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元