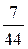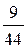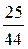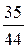题目内容
（本题满分12分）.设进入健身中心的每一位健身者选择甲种健身项目的概率是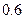
，选择乙种健身项目的概率是
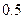，且选择甲种与选择乙种健身项目相互独立，各位健身者之间选择健身项目是相互独立的。
（Ⅰ）求进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率；
（Ⅱ）求进入该健身中心的4位健身者中，至少有2位既未选择甲种又未选择乙种健身项目的概率。
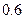，选择乙种健身项目的概率是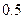，且选择甲种与选择乙种健身项目相互独立，各位健身者之间选择健身项目是相互独立的。（Ⅰ）求进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率；
（Ⅱ）求进入该健身中心的4位健身者中，至少有2位既未选择甲种又未选择乙种健身项目的概率。
0.5,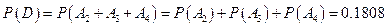
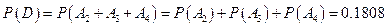
解：（Ⅰ）记A表示事件：进入该健身中心的1位健身者选择的是甲种项目，B表示事件：进入该健身中心的1位健身者选择的是乙种项目，则事件A与事件B相互独立，P（A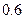）＝，P（B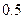）＝。―――－1分
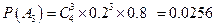
故进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率为：P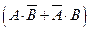
＝
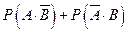＝P（A）
＋
＝
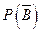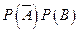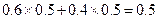。-――4分
（Ⅱ）记C表示事件：进入该健身中心的1位健身者既未选择甲种又未选择乙种健身项目，D表示事件：进入该健身中心的4位健身者中，至少有2位既未选择甲种又未选择乙种健身项目，A2表示事件：进入该健身中心的4位健身者中恰有2位既未选择甲种又未选择乙种健身项目，A3表示事件：进入该健身中心的4位健身者中恰有3位既未选择甲种又未选择乙种健身项目，A4表示事件：进入该健身中心的4位健身者中恰有4位既未选择甲种又未选择乙种健身项目，―――5分
则P（C）＝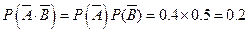
，―――7分
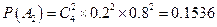，―――8分
，―――9分
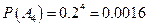―――10分
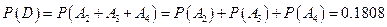。―――12分
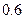，P（B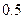）＝。―――－1分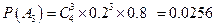故进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率为：P
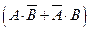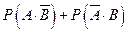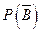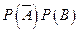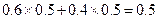＝＝P（A）＋＝。-――4分（Ⅱ）记C表示事件：进入该健身中心的1位健身者既未选择甲种又未选择乙种健身项目，D表示事件：进入该健身中心的4位健身者中，至少有2位既未选择甲种又未选择乙种健身项目，A2表示事件：进入该健身中心的4位健身者中恰有2位既未选择甲种又未选择乙种健身项目，A3表示事件：进入该健身中心的4位健身者中恰有3位既未选择甲种又未选择乙种健身项目，A4表示事件：进入该健身中心的4位健身者中恰有4位既未选择甲种又未选择乙种健身项目，―――5分
则P（C）＝
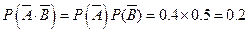，―――7分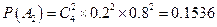，―――8分，―――9分
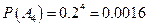―――10分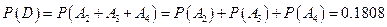。―――12分
练习册系列答案
同步拓展阅读系列答案
相关题目
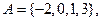在平面直角坐标系中，点M的坐标为(x,y) ，其中
。 
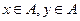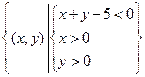上的概率。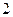
种服装商品, 
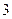种日用商品中,选出
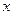元，同时,若顾客购买该商品,则允许有
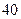元的奖券.假设顾客每次抽奖时获奖的概率都是
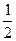,若使促销方案对商场有利，则
，师徒二人各加工2个零件都是精品的概率为
（I）求徒弟加工2个零件都是精品的概率；
，第二次出现的点数为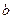
．
的概率；
，圆
，求直线
与圆
相离的概率。
