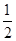已知函数f(x)=(13)x-log2x.正实数a.b.c是公差为正数的等差数列.且满足f＜0．若实数d是方程f(x)=0的一个解.那么下列四个判断:①d＜a,②d＜b,③d＜c,④d＞c中有可能成立的个数为( )A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f（x）=(

)x-log₂x，正实数a，b，c是公差为正数的等差数列，且满足f（a）f（b）f（c）＜0．若实数d是方程f（x）=0的一个解，那么下列四个判断：①d＜a；②d＜b；③d＜c；④d＞c中有可能成立的个数为（　　）

A．1

B．2

C．3

D．4

f（x）在（0，+∞）上单调减，值域为R又a＜b＜c，f（a）f（b）f（c）＜0，所以（1）若f（a），f（b）＞0，f（c）＜0．由f（d）=0知，a＜b＜d＜c，③成立；（2）若f（a），f（b），f（c）＜0．此时d＜a＜b＜c，①②③成立．综上，可能成立的个数为3．

练习册系列答案

在等差数列{a_n}中，3a₉-a₁₅-a₃=20，则2a₈-a₇的值为（　　）

已知数列{a_n}的前n项和为S_n，且an=Sn•Sn-1(n≥2，Sn≠0)，a1=

．
（Ⅰ）求证：数列{

}为等差数列；
（Ⅱ）求满足a_n＜0的自然数n的集合．

（大013•济宁二模）在△ABCb，A，B，C的对边分别为a，b，c，若acosC，bcosB，ccosA成等差数列，则B=（　　）

+1，若a，b，c成等差数列（公差不为零），则f（a）+f（c）=______．

在等差数列{a_n}中，a₃+a₄+a₅=12，那么a₂-a₄+a₆的值为（　　）

数列{a_n}中，a_n=3-2n，从第一项起各项依次为1，x，-3，y，…，那么x-y=（　　）

已知{a_n}是公比为q的等比数列，且a₁，a₃，a₂成等差数列，则q＝ ( ).

试题分类