题目内容
若存在正数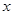 ,使
,使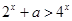 成立,则实数
成立,则实数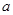 的取值范围是 .
的取值范围是 .
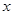 ,使
,使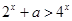 成立,则实数
成立,则实数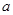 的取值范围是 .
的取值范围是 .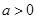
试题分析:∵存在正数
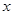 ,使
,使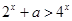 成立,∴
成立,∴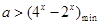 ,∴令
,∴令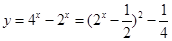 ,
,∵
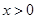 ,∴
,∴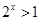 ,∴
,∴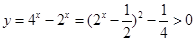 ,∴
,∴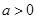 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
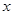 ,使
,使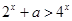 成立,则实数
成立,则实数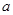 的取值范围是 .
的取值范围是 .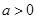
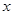 ,使
,使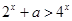 成立,∴
成立,∴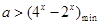 ,∴令
,∴令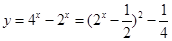 ,
,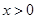 ,∴
,∴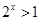 ,∴
,∴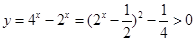 ,∴
,∴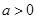 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案