题目内容
（本小题共10分）甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约
。甲表示只要面试合格就签约，乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是
，且面试是否合格互不影响，求：
①至少有1人面试合格的概率；
②签约人
数ξ的分布列和数学期望。
。甲表示只要面试合格就签约，乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是，且面试是否合格互不影响，求：①至少有1人面试合格的概率；
②签约人
数ξ的分布列和数学期望。①至少有1人面试合格的概率是
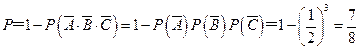
②ξ的分布列为
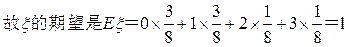
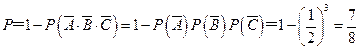
②ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  | |  | |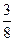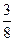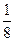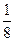
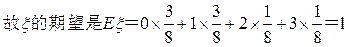
解：用A、B、C分别表示事件甲、乙、丙面试合格，
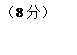
由题意知A、B、C相互独立，
且P（A）＝P（B）＝P（C）＝ （1分）
（Ⅰ）至少有1人面试合格的概率是
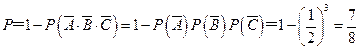（4分）
（Ⅱ）ξ的可能取值为0，1，2，3.
＝
＝
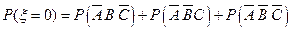
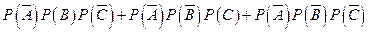
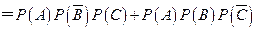
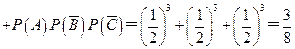
∴ξ的分布列为
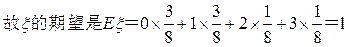（10分
）
由题意知A、B、C相互独立，
且P（A）＝P（B）＝P（C）＝ （1分）（Ⅰ）至少有1人面试合格的概率是
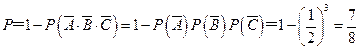（4分） （Ⅱ）ξ的可能取值为0，1，2，3.
＝
＝
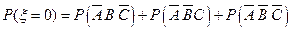
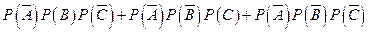
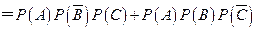
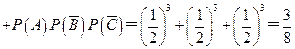
| ξ | 0 | 1 | 2 | 3 |
| P | | | | |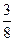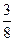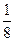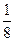
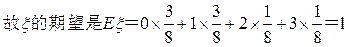（10分）
练习册系列答案
相关题目
，乙投篮命中的概率为
．
分，求乙所得分数
的概率分布和数学期望．
，用
表示这4位乘客在终点站下车的人数，求：
甲、乙、丙这3个展览馆的概率分别是0.4，0.5，0.6，且是否参观哪个展览馆互不影响，设
表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.
在区间
上单调递增”为事件
，求事件
3个旅游团提供甲、乙、丙、丁4条旅游线路，每个旅游团从中任选一条。
。这三项测试能否通过相互之间没有影响。试卷
的分布列如右方表格，