题目内容

（本小题满分12分）
某象棋教练用下列方式考核队员:任一名队员可以选择与一级棋士或二级棋士对奕,规定与一级棋士对奕取胜得3分,不胜得0分,与二级棋士对弈取胜得2分,不胜得0分,如果前两局得分超过3分即算考核合格,否则比赛三局.某位队员与一级棋士对弈获胜的概率为q1,与二级棋士对弈获胜的概率为0.6,该队员选择先与一级棋士对奕,以后都与二级棋士对奕,用X表示该队员考核结束后所得的总分,已知P(X=0)=0.128.
(1)求q1的值;
(2)写出随机变量X的分布列并求出数学期望EX;
(3)试比较该队员选择都与二级棋士对奕与上述方式最后得分大于3的概率的大小;
略

 P(X="3)=P(A)=" P(A)P()P()=×()2= (0.032)
P(X="4)=P(BB)=" P()P(B)P(B)=××= (0.288)
P(X="5)=P(AB+AB)=" P(AB)+P(AB)= P(A)P()P(B)+P(A)P(B)=××+×= (0.168)
所以随机变量X的分布列为
  X         
0          
2             
   3   
   4   
   5   
   p        
          
              
         
        
              
∴随机变量X的数学期望EX===2.856……………8分
练习册系列答案
相关题目
已知ξ～B（n，p），且Eξ=7，Dξ=6，则p等于
A．B．C．D．
．（本小题12 分）
有一个箱子内放有3个红球、1个白球、1个黄球，现从箱子里任意取球，每次只取一个，取后不放回.
①求前两次先后取到一个红球和一个白球的概率；
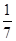
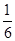
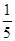
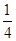
②若取得红球则停止取球，求取球次数的分布列及期望.
（本小题满分12分）
某同学参加3门课程的考试，假设该同学第一门课程取得优秀成绩的概率为。第二、第三门课程取得优秀成绩的概率均为，且不同课程是否取得优秀成绩相互独立。
（1）求该生恰有1门课程取得优秀成绩的概率；
（2）求该生取得优秀成绩的课程门数X的期望。
（本小题共10分）甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约。甲表示只要面试合格就签约，乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是，且面试是否合格互不影响，求：
①至少有1人面试合格的概率；
②签约人数ξ的分布列和数学期望。
设随机变量ξ～N(μ，σ2 )，且 P(ξ)= P(ξ)，则c ="(  " )（  C  ）
A．σ2B．σC．μD．–μ
（本题满分14分）某突发事件，在不采取任何预防措施的情况下发生的概率为，一旦发生，将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择，单独采用甲、乙预防措施所需的费用分别为40万元和20万元，采用相应预防措施后此突发事件不发生的概率分别为和.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用，请分别计算这几种预防方案的总费用，并指出哪一种预防方案总费用最少.
(注：总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
（本题12分）某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为为P1，P2，P3，又知P1，P2是方程25x2－15x＋a＝0的两个根，且P2＝P3，
（1）求P1，P2，P3的值；
（2）记表示销售两台这种家用电器的销售利润总和，求的分布列；
（3）求销售两台这种家用电器的销售利润总和的平均值。

（本小题满分12分）
一个口袋巾装有标号为1，2，3的6个小球，其中标号1的小球有1个，标号2的小球有2个，标号3的小球有3个，现从口袋中随机摸出2个小球．
（I）求摸出2个小球标号之和为3的概率；
（II）求摸出2个小球标号之和为偶数的概率；
（III）用表示摸出2个小球的标号之和，写出的分布列，并求的数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网