题目内容
若 ,函数
,函数 有零点的概率为
有零点的概率为
 ,函数
,函数 有零点的概率为
有零点的概率为A. | B. | C.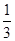 | D. |
D
分析:本题考查的知识点是几何概型的意义,关键是要找出函数f(x)=x2-2ax+b2有零点时对应的区域面积的大小,再将其与a∈[0,3],b∈[0,2]表示的面积大小一齐代入几何概型的计算公式进行解答.

解:函数f(x)=x2-2ax+b2有零点,则4a2-4b2≥0
即:
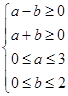 ,
,满足条件的区域如下图中阴影部分所示:
函数f(x)=x2-2ax+b2有零点的概率P=
 =
=
故选D.

练习册系列答案
相关题目


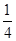

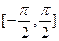 上随机取一个数
上随机取一个数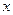 ,则
,则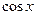 的值介于
的值介于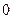 到
到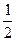 的概率是
的概率是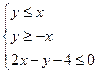 表示的平面区域为
表示的平面区域为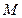 ,
,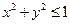 所表示的平面区域为
所表示的平面区域为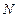 ,现随机向区域
,现随机向区域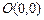 、
、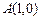 、
、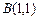 、
、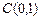 ,曲线
,曲线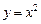 经过点
经过点 ,现将一质点随机投入正方形中,则质点落在图中阴影区域的概率是____________。
,现将一质点随机投入正方形中,则质点落在图中阴影区域的概率是____________。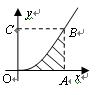
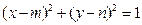 表示圆心在坐标轴上的圆的概率是 .
表示圆心在坐标轴上的圆的概率是 .



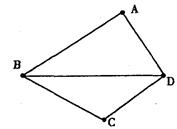
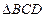 内的频率
内的频率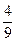 附近,那么点A和点C到直线BD的距离之比约为 .
附近,那么点A和点C到直线BD的距离之比约为 .