题目内容

设函数y=f（x）是定义在（0，+∞）上的减函数，并且满足f(xy)=f（x）+f（y），f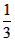（）=1，
（1）求f（1），f（3）的值；
（2）如果f（x）+f（2-x）<2，求x的取值范围。

解：（1）∵对任意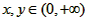，有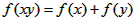
∴令x=y=1，则f（1）=f（1）+f（1），∴f（1）=0
∴令x=3，y=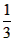，并由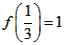，得f（1）=f（3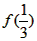）+=f（3）+1=0
得f（3）=-1
（2）∵对任意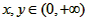，有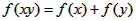
∴2=1+1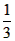=f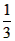（）+f（）=f（）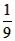
∴f（x）+f（2-x）=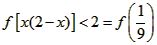
又∵y=f（x）是定义在R+上的减函数，
得：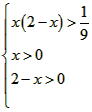
解之得：x∈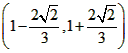

练习册系列答案
相关题目
设函数y=f （x）是定义域为R的奇函数，且满足f （x-2）=-f （x）对一切x∈R恒成立，当-1≤x≤1时，f （x）=x3，则下列四个命题：
①f（x）是以4为周期的周期函数．
②f（x）在[1，3]上的解析式为f （x）=（2-x）3．
③f（x）在(
3
2
，f(
3
2
))处的切线方程为3x+4y-5=0．
④f（x）的图象的对称轴中，有x=±1，其中正确的命题是（　　）
A、①②③B、②③④
C、①③④D、①②③④
设函数y=f（x）是定义在（0，+∞）上的函数，并且满足下面三个条件：
①对正数x、y都有f（xy）=f（x）+f（y）；
②当x＞1时，f（x）＜0；
③f（3）=-1
（I）求f（1）和f(
19
)的值；
（II）如果不等式f（x）+f（2-x）＜2成立，求x的取值范围．
设函数y=f（x）是定义在R上以1为周期的函数，若g（x）=f（x）-2x在区间[2，3]上的值域为[-2，6]，则函数g（x）在[-12，12]上的值域为（　　）
设函数y=f（x）是定义在正实数上的增函数，且f（xy）=f（x）+f（y），
（1）求证：f（
xy
）=f（x）-f（y）；
（2）若f（3）=1，f（a）＞f（a-1）+2，求a的取值范围．
设函数y=f（x）是定义在R上的奇函数，且f（x-2）=-f（x）对一切x∈R都成立，又当x∈[-1，1]时，f（x）=x3，则下列五个命题：
①函数y=f（x）是以4为周期的周期函数；
②当x∈[1，3]时，f（x）=（ x-2）3；
③直线x=±1是函数y=f（x）图象的对称轴；
④点（2，0）是函数y=f（x）图象的对称中心；
⑤函数y=f（x）在点（
3
2
，f（
3
2
））处的切线方程为3x-y-5=0．
其中正确的是
①③
①③
．（写出所有正确命题的序号）