题目内容
(2013•南京二模)设f(x)=(1+x)(1+2x)…(1+nx)(其中,n∈N*且n≥2),其展开后含xr项的系数记作ar(r=0,1,2,…,n).
(1)求a1(用含n的式子表示);
(2)求证:a2=
.
(1)求a1(用含n的式子表示);
(2)求证:a2=
| 3n+2 |
| 4 |
| C | 3 n+1 |
分析:(1)从函数的解析式的n个括号中,选一个x,余下的选常数,即可得到a1(用含n的式子表示);
(2)从函数的解析式的n个括号中,选两个x项,余下的选常数,即可得到a2,然后证明:a2=
.
(2)从函数的解析式的n个括号中,选两个x项,余下的选常数,即可得到a2,然后证明:a2=
| 3n+2 |
| 4 |
| C | 3 n+1 |
解答:解:(1)由题意从函数的解析式的n个括号中,选一个x,余下的选常数,
∴a1=1+2+…+n=
.
(2)由题意从函数的解析式的n个括号中,选两个含有x的项,余下的选常数,即可得到a2,
∴a2=1×1+1×2+1×3+…+1•n+2×3+2×4+…+2•n+…+(n-1)•n
=
=
[
]2-
=
•
=
∴a2=
.
∴a1=1+2+…+n=
| n(n+1) |
| 2 |
(2)由题意从函数的解析式的n个括号中,选两个含有x的项,余下的选常数,即可得到a2,
∴a2=1×1+1×2+1×3+…+1•n+2×3+2×4+…+2•n+…+(n-1)•n
=
| (1+2+…+n)2-(12+22+…+n2) |
| 2 |
=
| 1 |
| 2 |
| n(n+1) |
| 2 |
| n(n+1)(2n+1) |
| 12 |
=
| n(n+1) |
| 4 |
| (n-1)(3n+2) |
| 6 |
=
| 3n+2 |
| 4 |
| C | 3 n+1 |
∴a2=
| 3n+2 |
| 4 |
| C | 3 n+1 |
点评:本题考查二项式定理的应用,分析法以及综合法解决问题额方法,注意x的指数以及展开式项的关系是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
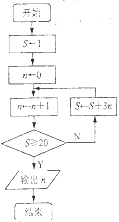 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是