题目内容
(2013•南京二模)盒子中有大小相同的3只白球、2只黑球,若从中随机地摸出两只球,则两只球颜色相同的概率是
.
| 2 |
| 5 |
| 2 |
| 5 |
分析:因为只是从盒子中摸出求,对3只白球和2只黑球标记后无需思考排序问题,用列举法写出从中随机地摸出两只球的所有摸法种数,查出两只球颜色相同的摸法种数,则两只球颜色相同的概率可求.
解答:解:记3只白球分别为白1,白2,白3,2只黑球分别记为黑1,黑2.
从中随机地摸出两只球,所有不同的摸法为(白1白2)(白1白3)(白1黑1)(白1黑2)(白2白3)(白2黑1)
(白2黑2)(白3黑1)(白3黑2)(黑1黑2)共10种,
其中两只球颜色相同的摸法有(白1白2)(白1白3)(白2白3)(黑1黑2)共4种,
所以两只球颜色相同的概率是p=
=
.
故答案为
.
从中随机地摸出两只球,所有不同的摸法为(白1白2)(白1白3)(白1黑1)(白1黑2)(白2白3)(白2黑1)
(白2黑2)(白3黑1)(白3黑2)(黑1黑2)共10种,
其中两只球颜色相同的摸法有(白1白2)(白1白3)(白2白3)(黑1黑2)共4种,
所以两只球颜色相同的概率是p=
| 4 |
| 10 |
| 2 |
| 5 |
故答案为
| 2 |
| 5 |
点评:本题考查了古典概型及其概率计算公式,考查了列举法列举随机事件的个数,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
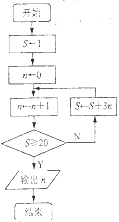 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是