题目内容
19. 如图,直线l为一森林的边界,AC⊥l,AC=6,B为AC的中点.野兔与狼分别于A、B同时匀速奔跑,其中野兔的速度是狼的两倍.如果狼比野兔提前或同时跑到某一点,则就认为野兔在这点能被狼抓住.野兔是沿着AD直线奔跑的.问直线l上的点D处在什么位置时,野兔在AD上不可能被狼抓住?
如图,直线l为一森林的边界,AC⊥l,AC=6,B为AC的中点.野兔与狼分别于A、B同时匀速奔跑,其中野兔的速度是狼的两倍.如果狼比野兔提前或同时跑到某一点,则就认为野兔在这点能被狼抓住.野兔是沿着AD直线奔跑的.问直线l上的点D处在什么位置时,野兔在AD上不可能被狼抓住?
分析 由题意,建立下面直角坐标系x0y,并设M(x,y),野兔在AD上不可能被狼则:$\frac{|BM|}{v}$>$\frac{|AM|}{2v}$由此不等式得出2|BM|>|AM|,用两点间距离公式将此不等式用坐标表示出来,整理出方程,利用点到直线的距离公式进行求解即可.
解答 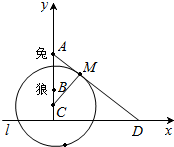 解:如图所示,建立平面直角坐标系x0y,并设M(x,y).
解:如图所示,建立平面直角坐标系x0y,并设M(x,y).
则A(0,6),B(0,3),D(a,0),(a>0)
野兔在AD上不可能被狼则:$\frac{|BM|}{v}$>$\frac{|AM|}{2v}$.
即2|BM|>|AM|
∴2$\sqrt{{x}^{2}+(y-3)^{2}}$>$\sqrt{{x}^{2}+(y-6)^{2}}$
两边平方,整理得:x2+y2-4y>0
即:x2+(y-2)2>4,
所以,野兔在AD上不可能被狼抓住的区域为圆的外部,
直线AD的方程为$\frac{x}{a}+\frac{y}{6}=1$,即6x+ay-6a=0,
圆心(0,2)到直线的距离d=$\frac{|0+2a-6a|}{\sqrt{{6}^{2}+{a}^{2}}}$=$\frac{|4a|}{\sqrt{36+{a}^{2}}}$>2,
平方得a2>12,
即a>2$\sqrt{3}$或a<-2$\sqrt{3}$(舍).
直线l上的点D处在距离大于2$\sqrt{3}$时,野兔在AD上不可能被狼抓住.
点评 本题考查求轨迹方程,由于题设条件比较抽象,解答本题,关键是建立起合适的模型,本题考查了以形助数能力及转化化归的能力,难度较大.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.下列不等式中成立的是( )
| A. | $sin(-\frac{π}{18})<sin(-\frac{π}{10})$ | B. | $sin\frac{5π}{3}>sin2$ | ||
| C. | $cos(-\frac{23}{5}π)>cos(-\frac{17}{4}π)$ | D. | $tan(-\frac{π}{5})>tan(-\frac{3π}{7})$ |
10.函数f(x)=ax3-x2+x-6在(-∞,+∞)上既有极大值又有极小值,则a的取值范围为( )
| A. | a>0 | B. | a<0 | C. | $a>\frac{1}{3}$ | D. | $a<\frac{1}{3}$且a≠0 |
14.α,β都是锐角,且sinα=$\frac{5}{13}$,cos(α+β)=-$\frac{4}{5}$,则cosβ的值是( )
| A. | -$\frac{33}{65}$ | B. | $\frac{16}{65}$ | C. | $\frac{56}{65}$ | D. | $\frac{63}{65}$ |