题目内容
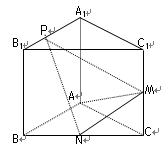
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在直线A1B1上,且![]()
(1)证明:无论![]() 入取何值,总有AM⊥PN;
入取何值,总有AM⊥PN;
(2)当![]() 入取何值时,直线PN与平面ABC所成的角θ最大?并求该角取最大值时的正切值。
入取何值时,直线PN与平面ABC所成的角θ最大?并求该角取最大值时的正切值。
(3)是否存在点P,使得平面PMN与平面ABC所成的二面角为30º,若存在,试确定点P的位置,若不存在,说明理由。
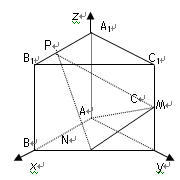
解:如图,以A为原点建立空间直角坐标系,
则A1(0,0,1),B1(1,0,1), M(0,1,![]() ),
),
 N(
N(![]() ,0)
,0)![]() ,
,
![]() ,
,![]()
(1)∵![]() ,∴
,∴![]()
∴无论![]() 取何值,AM⊥PN.........4分
取何值,AM⊥PN.........4分
(2)∵![]() (0,0,1)是平面ABC的一个法向量。
(0,0,1)是平面ABC的一个法向量。![]()
∴sinθ=|cos<![]() |=
|=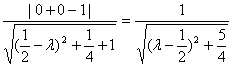
∴当![]() =
=![]() 时,θ取得最大值,此时sinθ=
时,θ取得最大值,此时sinθ=![]() ,cosθ=
,cosθ=![]() ,tanθ=2
,tanθ=2
当![]() =
=![]() 时,θ取得最大值,此时tanθ=2..........8分
时,θ取得最大值,此时tanθ=2..........8分
(3)设存在,![]() ,设
,设![]() 是平面PMN的一个法向量。
是平面PMN的一个法向量。
则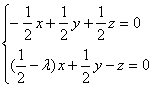 得
得 令x=3,得y=1+2
令x=3,得y=1+2![]() ,z=2-2
,z=2-2![]()
∴![]() ..........10分
..........10分
∴|cos<![]() >|=
>|=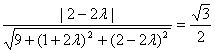 化简得4
化简得4![]()
∵△=100-4![]() 4
4![]() 13=-108<0∴方程(*)无解
13=-108<0∴方程(*)无解
∴不存在点P使得平面PMN与平面ABC所成的二面角为30º.........12分

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.