题目内容
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且| A1P |
| A1B1 |
(Ⅰ)证明:无论λ取何值,总有AM⊥PN;
(Ⅱ)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点P,使得平面PMN与平面ABC所成的二面角为30°,若存在,试确定点P的位置,若不存在,请说明理由.
分析:(1)以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,求出各点的坐标及对应向量的坐标,易判断
•
=0,即AM⊥PN;
(2)设出平面ABC的一个法向量,表达出sinθ,利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正切值;
(3)假设存在,利用平面PMN与平面ABC所成的二面角为30°,则平面PMN与平面ABC法向量的夹角为30°,代入向量夹角公式,可以构造一个关于λ的方程,研究方程根的情况,即可得到结论.
| AM |
| PN |
(2)设出平面ABC的一个法向量,表达出sinθ,利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的λ值,进而求出此时θ的正切值;
(3)假设存在,利用平面PMN与平面ABC所成的二面角为30°,则平面PMN与平面ABC法向量的夹角为30°,代入向量夹角公式,可以构造一个关于λ的方程,研究方程根的情况,即可得到结论.
解答: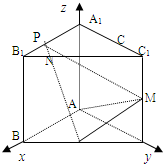 (1)证明:如图,以A为原点建立空间直角坐标系,则A1(0,0,1),
(1)证明:如图,以A为原点建立空间直角坐标系,则A1(0,0,1),
B1(1,0,1),M(0,1,
),N(
,
,0)
=λ
=λ(1,0,0)=(λ,0,0),
=
+
=(λ,0,1),
=(
-λ,
,-1)
(1)解:∵
=(0,1,
),∴
•
=0+
-
=0
∴无论λ取何值,AM⊥PN…(4分)
(2)解:∵
=(0,0,1)是平面ABC的一个法向量.
∴sinθ=|cos<
•
>|=
=
而θ∈[0,
],当θ最大时,sinθ最大,tanθ最大,θ=
除外,
∴当λ=
时,θ取得最大值,此时sinθ=
,cosθ=
,tanθ=2 …(8分)
(3)假设存在,则
=(-
,
,
),设
=(x,y,z)是平面PMN的一个法向量.
则
得
令x=3,得y=1+2λ,z=2-2λ
∴
=(3,1+2λ,2-2λ)
∴|cos<
,
>|=
=
化简得4λ2+10λ+13=0(*)
∵△=100-4×4×13=-108<0
∴方程(*)无解
∴不存在点P使得平面PMN与平面ABC所成的二面角为30°…(13分)
 (1)证明:如图,以A为原点建立空间直角坐标系,则A1(0,0,1),
(1)证明:如图,以A为原点建立空间直角坐标系,则A1(0,0,1),B1(1,0,1),M(0,1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A1P |
| A1B1 |
| AP |
| AA1 |
| A1P |
| PN |
| 1 |
| 2 |
| 1 |
| 2 |
(1)解:∵
| AM |
| 1 |
| 2 |
| AM |
| PN |
| 1 |
| 2 |
| 1 |
| 2 |
∴无论λ取何值,AM⊥PN…(4分)
(2)解:∵
| m |
∴sinθ=|cos<
| m |
| PN |
| |0+0-1| | ||||||
|
| 1 | ||||||
|
而θ∈[0,
| π |
| 2 |
| π |
| 2 |
∴当λ=
| 1 |
| 2 |
|
|
(3)假设存在,则
| NM |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
则
|
|
∴
| n |
∴|cos<
| m |
| n |
| |2-2λ| | ||
|
| ||
| 2 |
∵△=100-4×4×13=-108<0
∴方程(*)无解
∴不存在点P使得平面PMN与平面ABC所成的二面角为30°…(13分)
点评:利用向量知识解决立体几何问题的优点在于用代数化的方法解决立体几何,解题的关键在于用坐标表示空间向量,熟练掌握向量夹角公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.