题目内容
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.(1)求证:BD⊥AC1;
(2)若AB=
| 2 |
| 3 |
分析:(1)先根据AA1⊥平面ABC证得AA1⊥BD;再结合AB=BC,D为AC中点得到AC⊥BD;两个结论相结合即可得BD⊥平面ACC1 A1进而得到结论;
(2)根据AA1⊥平面ABC,可得CC1⊥平面ABC,进而得到AC1与平面ABC所成的角为∠C1AC;然后在RT△C1CA中求出∠C1AC即可得到结论.
(2)根据AA1⊥平面ABC,可得CC1⊥平面ABC,进而得到AC1与平面ABC所成的角为∠C1AC;然后在RT△C1CA中求出∠C1AC即可得到结论.
解答: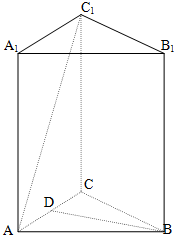 解:(1)证明:∵AA1⊥平面ABC,∴AA1⊥BD
解:(1)证明:∵AA1⊥平面ABC,∴AA1⊥BD
又∵AB=BC,D为AC中点,∴AC⊥BD
∴BD⊥平面ACC1 A1
∴BD⊥AC1…(4分)
(2)∵AA1⊥平面ABC,∴CC1⊥平面ABC
∴AC1与平面ABC所成的角为∠C1AC
∵AB=BC,∠ABC=90°,AB=
,∴AC=2
又AA1=2
,∴CC1=2
∴tan∠C1AC=
=
=
,
∴∠C1AC=60°.
即AC1与平面ABC所成的角为60°…(8分)
 解:(1)证明:∵AA1⊥平面ABC,∴AA1⊥BD
解:(1)证明:∵AA1⊥平面ABC,∴AA1⊥BD又∵AB=BC,D为AC中点,∴AC⊥BD
∴BD⊥平面ACC1 A1
∴BD⊥AC1…(4分)
(2)∵AA1⊥平面ABC,∴CC1⊥平面ABC
∴AC1与平面ABC所成的角为∠C1AC
∵AB=BC,∠ABC=90°,AB=
| 2 |
又AA1=2
| 3 |
| 3 |
∴tan∠C1AC=
| CC1 |
| AC |
2
| ||
| 2 |
| 3 |
∴∠C1AC=60°.
即AC1与平面ABC所成的角为60°…(8分)
点评:本题主要考查直线与平面所成的角以及直线和直线垂直的判定.一般在证明线线垂直时,先证明线面垂直;而在证明线面垂直时,先证明线线垂直.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|