题目内容
若直线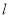 过点
过点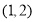 且垂直于直线
且垂直于直线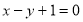 ,则直线
,则直线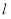 的斜截式方程是 .
的斜截式方程是 .
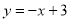
【解析】
试题分析:过点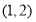 且垂直于直线
且垂直于直线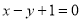 的直线方程为
的直线方程为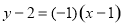 ,即
,即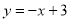 .
.
考点:直线的方程,两条直线的位置关系.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
题目内容
若直线 过点
过点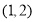 且垂直于直线
且垂直于直线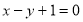 ,则直线
,则直线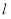 的斜截式方程是 .
的斜截式方程是 .
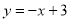
【解析】
试题分析:过点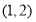 且垂直于直线
且垂直于直线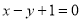 的直线方程为
的直线方程为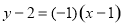 ,即
,即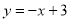 .
.
考点:直线的方程,两条直线的位置关系.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案