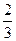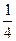题目内容
两人相约在7:30到8:00之间相遇,早到者应等迟到者10分钟方可离去,如果两人出发是各自独立的,在7:30到8:00之间的任何时刻是等可能的,问两人相遇的可能性有多大______.
视30分钟为一个单位1.设两人到达约会地点的时刻分别为x,y,依题意,必须满足|x-y|≤
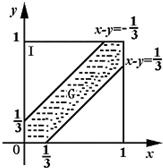
才能相遇.我们把他们到达的时刻分别作为横坐标和纵坐标,于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,如图所示,而相遇现象则发生在阴影区域G内,即甲、乙两人的到达时刻(x,y)满足|x-y|≤
,所以两人相遇的概率为区域G与区域Ⅰ的面积之比:
P=
=
=
.
故答案为:
.
| 1 |
| 3 |
| 1 |
| 3 |
P=
| S阴影 |
| S正方形 |
1-(
| ||
| 1 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |


练习册系列答案
相关题目
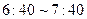 之间把报纸送到家,若小王每天在
之间把报纸送到家,若小王每天在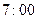 准时离家上班,则小王离家前能拿到报纸的概率( )
准时离家上班,则小王离家前能拿到报纸的概率( )