题目内容
【题目】已知集合M={(x,y)|f(x,y)=0},若对任意P1(x1 , y1)∈M,均不存在P2(x2 , y2)∈M使得x1x2+y1y2=0成立,则称集合M为“好集合”,下列集合为“好集合”的是( )
A.M={(x,y)|y﹣lnx=0}
B.M={(x,y)|y﹣![]() x2﹣1=0}
x2﹣1=0}
C.M={(x,y)|(x﹣2)2+y2﹣2=0}
D.M={(x,y)|x2﹣2y2﹣1=0}
【答案】D
【解析】解:由x1x2+y1y2=0得OP1⊥OP2 , 即存在两点与原点连线互相垂直;
A.取(e,1)∈M,(![]() )∈M,有
)∈M,有![]() ;
;
B.取(2,2),(﹣2,2)∈M,有2(﹣2)+22=0;
C.取(1,1),(1,﹣1),有11+1(﹣1)=0;
D.x2﹣2y2=1,渐近线方程为:![]() , 容易知道这两条渐近线夹角小于90°,所以不存在两点和原点的连线相互垂直,即该选项正确.
, 容易知道这两条渐近线夹角小于90°,所以不存在两点和原点的连线相互垂直,即该选项正确.
故选D.
【考点精析】本题主要考查了子集与真子集和集合的并集运算的相关知识点,需要掌握任何一个集合是它本身的子集;n个元素的子集有2n个,n个元素的真子集有2n -1个,n个元素的非空真子集有2n-2个;并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立才能正确解答此题.
B,反之也成立才能正确解答此题.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查者100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图,若日销量不低于50件,则称当日为“畅销日”.
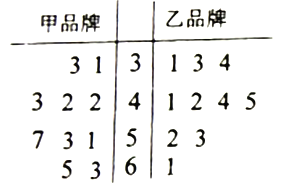
(1)现从甲品牌日销量大于40且小于60的样本中任取两天,求这两天都是“畅销日”的概率;
(2)用抽取的样本估计这100天的销售情况,请完成这两种品牌100天销量的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为品牌与“畅销日”天数有关.
的把握认为品牌与“畅销日”天数有关.
附: 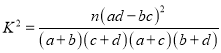 (其中
(其中![]() )
)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
畅销日天数 | 非畅销日天数 | 合计 | |
甲品牌 | |||
乙品牌 | |||
合计 |
【题目】长春市的“名师云课”活动自开展以来获得广大家长和学子的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给广大学子,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.