题目内容
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.

(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.
【答案】
见解析。
【解析】
试题分析:(I)通过证明BC⊥AD,通过AD⊥SC,BC∩SC=C,证明AD⊥平面SBC;
(II)过D作DE∥BC,交SB于E,E点即为所求.直接利用直线与平面平行的判定定理即可证明BC∥平面ADE.
(Ⅰ)证明: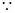 BC⊥平面SAC,AD
BC⊥平面SAC,AD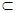 平面SAC,∴BC⊥AD,
平面SAC,∴BC⊥AD,
又∵AD⊥SC,
BC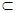 平面SBC, SC
平面SBC, SC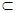 平面SBC,
平面SBC,
BC SC=C,
SC=C,
∴AD⊥平面SBC. …………(6分)
(Ⅱ)过A作AE⊥SB,交SB于E,E点即为所求.
∵AD⊥平面SBC,SB 平面SBC,
平面SBC,
∴AD⊥SB.
又AE⊥SB,AE AD=A
AD=A
∴SB⊥平面ADE,又SB 平面ABS,由两个平面垂直的判定定理知:
平面ABS,由两个平面垂直的判定定理知:
平面ABS⊥平面ADE…………(13分)考点:本题主要考查了直线与平面垂直,直线与平面平行的判定定理的应用,考查空间想象能力,逻辑推理能力.
点评:解决该试题的关键是熟练的运用线面垂直的判定定理和面面垂直的判定定理来证明命题的成立。

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和