题目内容
3.已知函数y=tan($\frac{1}{2}$x-$\frac{π}{6}$).(1)作出此函数在一个周期开区间上的简图;
(2)求出此函数的定义域、周期和单调区间;
(3)写出此函数图象的渐近线方程和所有对称中心的坐标.
分析 (1)利用五点作图法即可作出此函数在一个周期开区间上的简图;
(2)根据正切函数的性质即可求出此函数的定义域、周期和单调区间;
(3)根据渐近线方程和所有对称中心的性质进行求解即可.
解答 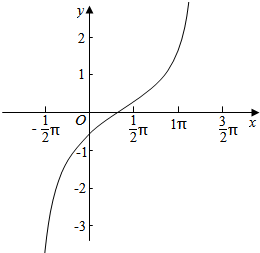 解:(1)作出此函数在一个周期开区间上的简图;
解:(1)作出此函数在一个周期开区间上的简图;
| $\frac{1}{2}$x-$\frac{π}{6}$ | -$\frac{π}{2}$ | -$\frac{π}{3}$ | 0 | $\frac{π}{3}$ | $\frac{π}{2}$ |
| x | -$\frac{2π}{3}$ | -$\frac{π}{3}$ | $\frac{π}{3}$ | π | $\frac{4π}{3}$ |
| y | -∞ | -$\sqrt{3}$ | 0 | $\sqrt{3}$ | +∞ |
(2)由$\frac{1}{2}$x-$\frac{π}{6}$≠kπ+$\frac{π}{2}$,得x≠2kπ+$\frac{4π}{3}$,
即函数的定义域为{x|x≠2kπ+$\frac{4π}{3}$,k∈Z},
函数的周期T=$\frac{π}{\frac{1}{2}}=2π$.
由kπ-$\frac{π}{2}$<$\frac{1}{2}$x-$\frac{π}{6}$<kπ+$\frac{π}{2}$,k∈Z,
得2kπ-$\frac{2π}{3}$<x<2kπ+$\frac{4π}{3}$,k∈Z,
即函数的单调递增区间为(2kπ-$\frac{2π}{3}$,2kπ+$\frac{4π}{3}$),k∈Z;
(3)由$\frac{1}{2}$x-$\frac{π}{6}$=kπ+$\frac{π}{2}$,得x=2kπ+$\frac{4π}{3}$,
即函数图象的渐近线方程为x=2kπ+$\frac{4π}{3}$,k∈Z,
由$\frac{1}{2}$x-$\frac{π}{6}$=$\frac{kπ}{2}$得x=kπ+$\frac{π}{3}$,k∈Z
即所有对称中心的坐标为(kπ+$\frac{π}{3}$,0).
点评 本题主要考查正切函数的图象和性质,要求熟练掌握正切函数的定义域,单调性,周期以及对称性的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知集合A={(x,y)|y=x2}.集合B={(x,y)|y=a},则“a>0”是集合A∩B中有2个元素的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |