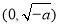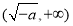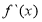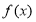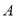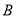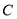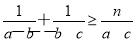题目内容
已知函数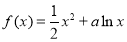 (
(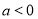 ).
).
(1)若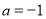 ,求函数
,求函数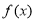 的极值;
的极值;
(2)若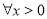 ,不等式
,不等式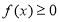 恒成立,求实数
恒成立,求实数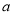 的取值范围.
的取值范围.
(1) 在
在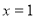 处有极小值
处有极小值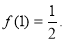 ;(2)
;(2) .
.
【解析】
试题分析:(1)求极值分三步:首先对函数求导,然后判断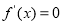 的根是否为极值点,最后求出极值;
的根是否为极值点,最后求出极值;
(2)要使 ,不等式
,不等式 恒成立,只要先利用导数求出
恒成立,只要先利用导数求出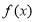 的最小值,然后使
的最小值,然后使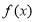 最小值大于等于零即可.
最小值大于等于零即可.
试题解析:【解析】
(1)当 时,
时,
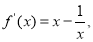 2分
2分
令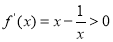 ,解得
,解得 ,所以
,所以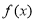 的单调增区间为(1,+∞);4分
的单调增区间为(1,+∞);4分
 ,解得
,解得 ,所以
,所以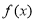 的单调减区间为(0,1)..5分
的单调减区间为(0,1)..5分
所以函数 在
在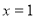 处有极小值
处有极小值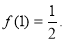 ..6分
..6分
(2)∵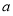 <0,由
<0,由 .令
.令
列表:
|
|
|
|
| _ | 0 | + |
| 减函数 | 极小值 | 增函数 |
8分
这是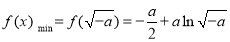 .10分
.10分
∵ ,不等式
,不等式 恒成立,∴
恒成立,∴ ,∴
,∴ ,
,
∴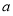 范围为
范围为 ..12分
..12分
考点:1.利用导数求极值最值;2.恒成立问题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目