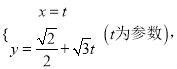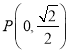题目内容
【题目】求与直线3x-4y+7=0平行，且在两坐标轴上截距之和为1的直线l的方程.
【答案】3x-4y-12=0.
【解析】试题分析: 方法一：由题意知：可设l的方程为3x-4y+m=0，求出l在x轴，y轴上的截距,由截距之和为1,解出m,代回求出直线方程; 方法二：设直线方程为
+
=1，由题意得
解出a,b即可.
试题解析:
方法一：由题意知：可设l的方程为3x-4y+m=0，
则l在x轴，y轴上的截距分别为-
， 
.
由-
+
=1知，m=-12.
所以直线l的方程为：3x-4y-12=0.
方法二：设直线方程为
+
=1，
由题意得
解得
所以直线l的方程为： 
+
=1.
即3x-4y-12=0.
点睛:本题考查直线方程的求法,属于基础题.直线方程有五种不同的形式:斜截式,点斜式,两点式,截距式和一般式,两种不同的方法分别使用了直线方程中的一般式和截距式,求出直线的横纵截距,根据题中给出的截距和为1,求出参数的值,代入原方程求出直线方程,最后写成一般形式.
练习册系列答案
相关题目
【题目】某公司有
五辆汽车，其中
两辆汽车的车牌尾号均为1. 
两辆汽车的车牌尾号均为2， 
车的车牌尾号为6，已知在非限行日，每辆车可能出车或不出车， 
三辆汽车每天出车的概率均为
， 
两辆汽车每天出车的概率均为
，且五辆汽车是否出车相互独立，该公司所在地区汽车限行规定如下：
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
（1）求该公司在星期一至少有2辆汽车出国的概率；
（2）设
表示该公司在星期二和星期三两天出车的车辆数之和，求
的分布列及期望.
