题目内容
等差数列{an}中,a1=1,a7=4,在等比数列{bn}中,b1=6,b2=a3,则满足bna26<1的最小正整数n是 .
6
试题分析:因为等差数列{an}中,a1=1,a7=4,那么可知1+6d=4,d=
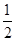 ,
,∵数列{bn}是等比数列,且b1=6,b2=a3,∴6q=1+2×
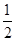 ,解得q=
,解得q=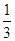 ,因为∵bna26<1,
,因为∵bna26<1,即可知
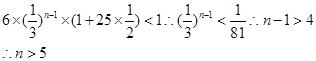
故最小的正整数为6,故答案为6.
点评:该试题考查等差数列、等比数列的基本量、通项,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错。

练习册系列答案
相关题目
 的前n项和分别是
的前n项和分别是


 }的前n项和为
}的前n项和为 ,已知
,已知 ,
, .
.
 ,求数列{
,求数列{ }的前项和
}的前项和 .
. 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意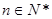 ,总有
,总有 成等差数列.
成等差数列. ,求数列
,求数列 的前
的前 .
. 的前n项和为Sn=2n2,
的前n项和为Sn=2n2, 为等比数列,且
为等比数列,且
 ,求数列
,求数列 前n项和Tn.
前n项和Tn.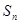 是数列
是数列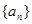 的前
的前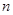 项和,若
项和,若 ,则数列
,则数列 ,则
,则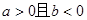
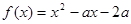 ,若存在
,若存在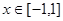 ,使得
,使得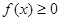 成立,则
成立,则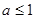
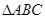 中,
中,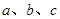 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若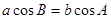 则
则 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命 ;
;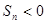 中,
中, 最大;
最大; 的
的 的个数有11个;
的个数有11个; ;
; 的前n项和为
的前n项和为 ,令
,令 ,称
,称 为数列
为数列 ,
, ,……,
,……,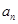 的“理想数”,已知数列
的“理想数”,已知数列 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2,  的前三项为
的前三项为 ,
, ,
,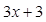 ,则
,则