题目内容
点O是平面α内的定点,点A(与点O不同)的“对偶点”A′是指:点A′在射线OA上且|OA|•|OA′|=1厘米2.若平面α内不同四点P,Q,R,S在某不过点O的直线l上,则它们相应的“对偶点”P′,Q′R′,S′在( )
分析:过O作与直线l垂直的直线m,以O为原点,直线m为x轴,单位为1厘米,建立平面直角平面坐标系,设出P,P′的坐标,利用|OP|•|OP′|=1,化简可得结论.
解答:解:过O作与直线l垂直的直线m,以O为原点,直线m为x轴,单位为1厘米,建立平面直角平面坐标系.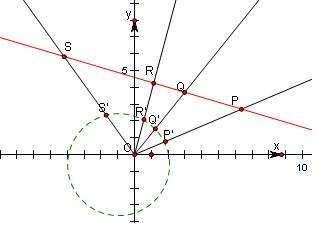
设直线l:x=
(a≠0),P(
,y0)是直线l上任意一点,它的“对偶点”为P′(x,y),则存在λ>0,使得
=λ
,即
=λx,y0=λy,
又|OP|•|OP′|=
•
=
+y0y=1,消去λ,得x2+y2-ax=0.
故P′,Q′R′,S′在过点O的圆x2+y2-ax=0上.
故选A.

设直线l:x=
| 1 |
| a |
| 1 |
| a |
| OP |
| OP′ |
| 1 |
| a |
又|OP|•|OP′|=
| OP |
| OP′ |
| x |
| a |
故P′,Q′R′,S′在过点O的圆x2+y2-ax=0上.
故选A.
点评:本题考查轨迹方程,考查新定义,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
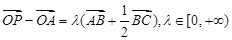 ,则直线AP一定过△ABC的( )
,则直线AP一定过△ABC的( )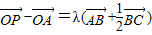 ,λ∈[0,+∞),则点P的轨迹一定过△ABC的( )
,λ∈[0,+∞),则点P的轨迹一定过△ABC的( ) ,λ∈[0,+∞),则点P的轨迹一定过△ABC的( )
,λ∈[0,+∞),则点P的轨迹一定过△ABC的( )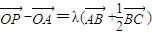 ,λ∈[0,+∞),则点P的轨迹一定过△ABC的( )
,λ∈[0,+∞),则点P的轨迹一定过△ABC的( )