题目内容
已知A,B,C三点不在同一条直线上,O是平面ABC内一定点,P是△ABC内的一
动点,若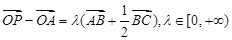 ,则直线AP一定过△ABC的( )
,则直线AP一定过△ABC的( )
A.重心 B.垂心 C.外心 D.内心
【答案】
A
【解析】
试题分析:取BC的中点D,连接AD,因为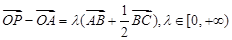 ,所以
,所以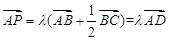 ,又λ∈[0,+∞),所以P点在射线AD上,故P的轨迹过△ABC的重心。故选A。
,又λ∈[0,+∞),所以P点在射线AD上,故P的轨迹过△ABC的重心。故选A。
考点:向量的运算;共线向量;三角形的五心。
点评:本题主要考查向量的运算法则、向量共线的充要条件、三角形的重心定义。设出BC的中点D,利用向量的运算法则化简 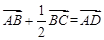 ,据向量共线的充要条件得到P在三角形的中线上是做此题的关键。三角形的重心定义:三条中线的交点。
,据向量共线的充要条件得到P在三角形的中线上是做此题的关键。三角形的重心定义:三条中线的交点。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
已知A、B、C三点不共线,且点O满足
+
+
=0,则下列结论正确的是( )
| OA |
| OB |
| OC |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|