题目内容
AB是圆O的直径，F为圆O上一点，∠BAF的角平分线与圆O交于点C，过点C作圆O的切线与直线AF相交于点D，若AB=6，∠DAB=
．
（1）求证：AD⊥CD；
（2）求DF•DA的值．
| π | 3 |
（1）求证：AD⊥CD；
（2）求DF•DA的值．
分析：（1）由AB是圆O的直径，可得∠ACB=
．由于∠DAB=
，AC平分∠DAB．利用角平分线的性质可得∠CAB=∠CAD=
，可得∠ABC=
．利用切线的性质可得∠ACD=∠ABC=
．可得∠ADC=
．即可．
（2）在Rt△ABC中，利用AB=6，∠ABC=
．可得AC=AB•sin
．在Rt△ACD中，DC=AC•cos∠ACD．再利用切割线定理可得：DF•DA=DC2即可．
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
（2）在Rt△ABC中，利用AB=6，∠ABC=
| π |
| 3 |
| π |
| 3 |
解答：（1）证明：如图所示．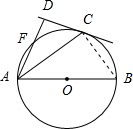
∵AB是圆O的直径，∴∠ACB=
．
∵∠DAB=
，AC平分∠DAB．
∴∠CAB=∠CAD=
，∴∠ABC=
．
∵DC与⊙O相切于点C，∴∠ACD=∠ABC=
．
∴∠CAD+∠ACD=
．
∴∠ADC=
．
∴AD⊥DC．
（2）在Rt△ABC中，∵AB=6，∠ABC=
．
∴AC=AB•sin
=3
．
在Rt△ACD中，DC=AC•cos∠ACD=3
×
=
．
由切割线定理可得：DF•DA=DC2=(
)2=
．
∵AB是圆O的直径，∴∠ACB=
| π |
| 2 |
∵∠DAB=
| π |
| 3 |
∴∠CAB=∠CAD=
| π |
| 6 |
| π |
| 3 |
∵DC与⊙O相切于点C，∴∠ACD=∠ABC=
| π |
| 3 |
∴∠CAD+∠ACD=
| π |
| 2 |
∴∠ADC=
| π |
| 2 |
∴AD⊥DC．
（2）在Rt△ABC中，∵AB=6，∠ABC=
| π |
| 3 |
∴AC=AB•sin
| π |
| 3 |
| 3 |
在Rt△ACD中，DC=AC•cos∠ACD=3
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
由切割线定理可得：DF•DA=DC2=(
3
| ||
| 2 |
| 27 |
| 4 |
点评：本题中考查了圆的性质、切线的性质、直角三角形的边角关系、角平分线的性质、切割线定理等基础知识与基本技能，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
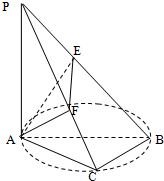如图，AB是圆O的直径，C是圆O上的点，PA垂直于圆O所在平面，AE⊥PB于E，AF⊥PC于F
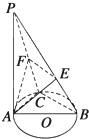如图，PA⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E、F分别是PB、PC上的点，AE⊥PB，AF⊥PC，给出下列结论：
如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DBCE为平行四边形，EC⊥平面ABC，AB=2AC=2，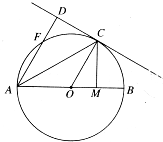
如图，AB是圆O的直径，C，F是圆O上的两点，AF∥OC，过C作圆O的切线交AF的延长线于点D．