题目内容
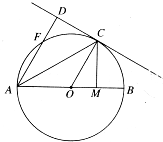 如图,AB是圆O的直径,C,F是圆O上的两点,AF∥OC,过C作圆O的切线交AF的延长线于点D.
如图,AB是圆O的直径,C,F是圆O上的两点,AF∥OC,过C作圆O的切线交AF的延长线于点D.(Ⅰ)证明:∠DAC=∠BAC;
(Ⅱ)若CM⊥AB,垂足为M,求证:AM•MB=DF•DA.
分析:(Ⅰ)AF∥OC⇒∠CAF=∠ACO,OA=OC⇒∠CAO=∠ACO,根据相等的传递性,得出∠DAC=∠BAC.
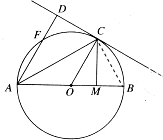
(Ⅱ)连接BC,在RT△ACB中,CM2=AM•MB,又CD为圆O的切线,所以CD2=DF•DA,只需证出CD=CM即可.根据圆的切线性质,OC⊥CD,结合AD∥OC得出AD⊥CD,从而可以证出RT△AMC≌△RTADC,CM=CD.
(Ⅱ)连接BC,在RT△ACB中,CM2=AM•MB,又CD为圆O的切线,所以CD2=DF•DA,只需证出CD=CM即可.根据圆的切线性质,OC⊥CD,结合AD∥OC得出AD⊥CD,从而可以证出RT△AMC≌△RTADC,CM=CD.
解答:证明:(Ⅰ)∵AF∥OC,∴∠CAF=∠ACO.
又∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAF=∠CAB,即∠DAC=∠BAC.
(Ⅱ)连接BC,在RT△ACB中,CM⊥AB,
∴CM2=AM•MB
又CD为圆O的切线,∴CD2=DF•DA
∵OC⊥CD,AD∥OC,∴AD⊥CD.
∴RT△AMC≌△RTADC,∴CM=CD
∴AM•MB=DF•DA.
又∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAF=∠CAB,即∠DAC=∠BAC.
(Ⅱ)连接BC,在RT△ACB中,CM⊥AB,
∴CM2=AM•MB
又CD为圆O的切线,∴CD2=DF•DA
∵OC⊥CD,AD∥OC,∴AD⊥CD.
∴RT△AMC≌△RTADC,∴CM=CD
∴AM•MB=DF•DA.

点评:本题考查的知识点是与圆相关的比例线段,由证明的结论形式分析证明思路,先分析角\边的关系,再选取恰当的公式、定理、性质是解答此类问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目


 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.



 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数