题目内容
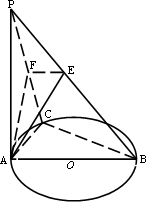
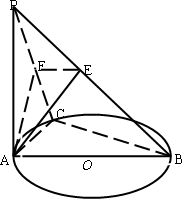
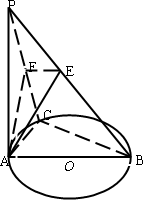
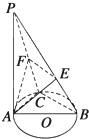 如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是PB、PC上的点,AE⊥PB,AF⊥PC,给出下列结论:
如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是PB、PC上的点,AE⊥PB,AF⊥PC,给出下列结论:①AF⊥PB;
②EF⊥PB;
③AF⊥BC;
④AE⊥平面PBC.
其中正确结论的序号是
①②③
①②③
.分析:PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点⇒BC⊥平面PAC,继而可证BC⊥AF,AF⊥PC,从而易证AF⊥平面PBC,从而可对①②③④作出判断.
解答:解:∵PA⊥圆O所在的平面α,BC?α,
∴PA⊥BC,
AB是圆O的直径,C是圆O上的一点,
∴BC⊥AC,
又PA∩AC=A,
∴BC⊥平面PAC,AF?平面PAC,
∴BC⊥AF,又AF⊥PC,PC∩BC=C,
∴AF⊥平面PBC,PB?平面PBC,
∴AF⊥PB,即①正确;
又AE⊥PB,同理可证PB⊥平面AFE,EF?平面AFE,
∴EF⊥PB,即②正确;
由BC⊥平面PAC,AF?平面PAC知,BC⊥AF,即③正确;
∵AF⊥平面PBC(前边已证),AE∩AF=A,
∴AE不与平面PBC垂直,故④错误,
综上所述,正确结论的序号是①②③.
故答案为:①②③.
∴PA⊥BC,
AB是圆O的直径,C是圆O上的一点,
∴BC⊥AC,
又PA∩AC=A,
∴BC⊥平面PAC,AF?平面PAC,
∴BC⊥AF,又AF⊥PC,PC∩BC=C,
∴AF⊥平面PBC,PB?平面PBC,
∴AF⊥PB,即①正确;
又AE⊥PB,同理可证PB⊥平面AFE,EF?平面AFE,
∴EF⊥PB,即②正确;
由BC⊥平面PAC,AF?平面PAC知,BC⊥AF,即③正确;
∵AF⊥平面PBC(前边已证),AE∩AF=A,
∴AE不与平面PBC垂直,故④错误,
综上所述,正确结论的序号是①②③.
故答案为:①②③.
点评:不同考查命题的真假判断与应用,着重考查线面垂直的判定与线面垂直的性质定理,考查推理与证明的能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是