题目内容
11.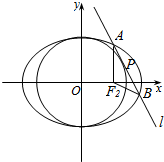 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,F1、F2分别为其左、右焦点,点M为椭圆C的上的顶点,且,△MF1F2的面积为2$\sqrt{5}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,F1、F2分别为其左、右焦点,点M为椭圆C的上的顶点,且,△MF1F2的面积为2$\sqrt{5}$.(1)求椭圆C的方程;
(2)如图,过圆x2+y2=b2上一点P(点P在y轴右侧),作该圆的切线l,交椭圆C于A,B两点,求△AF2B的周长.
分析 (1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{2}{3}}\\{\frac{1}{2}•2c•b=2\sqrt{5}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解出即可得出.
(2)设切点P(x0,y0),(x0>0).切线l的方程为:y-y0=-$\frac{{x}_{0}}{{y}_{0}}$(x-x0),A(x1,y1),B(x2,y2).${x}_{0}^{2}+{y}_{0}^{2}$=5.直线l的方程与椭圆方程联立可得:$(5{y}_{0}^{2}+9{x}_{0}^{2})$x2-90x0x+225-45${y}_{0}^{2}$=0,利用根与系数的关系可得:|AB|=$\sqrt{(1+\frac{{x}_{0}^{2}}{{y}_{0}^{2}})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,|AF2|=$\sqrt{{y}_{1}^{2}+({x}_{1}-2)^{2}}$,|BF2|=3-$\frac{2}{3}{x}_{2}$.即可得出△AF2B的周长=|AF2|+|BF2|+|AB|.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{2}{3}}\\{\frac{1}{2}•2c•b=2\sqrt{5}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=3,c=2,b2=5.
∴椭圆C的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$.
(2)设切点P(x0,y0),(x0>0).切线l的方程为:y-y0=-$\frac{{x}_{0}}{{y}_{0}}$(x-x0),A(x1,y1),B(x2,y2).
${x}_{0}^{2}+{y}_{0}^{2}$=5.
联立$\left\{\begin{array}{l}{y=-\frac{{x}_{0}}{{y}_{0}}x+\frac{5}{{y}_{0}}}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,化为:$(5{y}_{0}^{2}+9{x}_{0}^{2})$x2-90x0x+225-45${y}_{0}^{2}$=0,
∴x1+x2=$\frac{90{x}_{0}}{5{y}_{0}^{2}+9{x}_{0}^{2}}$=$\frac{90{x}_{0}}{25+4{x}_{0}^{2}}$,x1x2=$\frac{225-45{y}_{0}^{2}}{5{y}_{0}^{2}+9{x}_{0}^{2}}$=$\frac{45{x}_{0}^{2}}{25+4{x}_{0}^{2}}$.
∴|AB|=$\sqrt{(1+\frac{{x}_{0}^{2}}{{y}_{0}^{2}})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{\frac{5}{{y}_{0}^{2}}[(\frac{90{x}_{0}}{25+4{x}_{0}^{2}})^{2}-\frac{180{x}_{0}^{2}}{25+4{x}_{0}^{2}}]}$=$\frac{60{x}_{0}}{25+4{x}_{0}^{2}}$
|AF2|=$\sqrt{{y}_{1}^{2}+({x}_{1}-2)^{2}}$=$\sqrt{5(1-\frac{{x}_{1}^{2}}{9})+({x}_{1}-2)^{2}}$=3-$\frac{2}{3}{x}_{1}$,
同理可得|BF2|=3-$\frac{2}{3}{x}_{2}$.
∴△AF2B的周长=|AF2|+|BF2|+|AB|=3-$\frac{2}{3}{x}_{2}$+3-$\frac{2}{3}{x}_{1}$+$\frac{60{x}_{0}}{25+4{x}_{0}^{2}}$=6-$\frac{2}{3}$×$\frac{90{x}_{0}}{25+4{x}_{0}^{2}}$+$\frac{60{x}_{0}}{25+4{x}_{0}^{2}}$=6.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次的方程的根与系数的关系、两点之间的距离公式,考查了推理能力与计算能力,属于难题.

| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
| A. | $\frac{1}{4}$ | B. | $4\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | 64 |
| A. | 8个 | B. | 9个 | C. | 5个 | D. | 6个 |