题目内容
已知非负实数x，y满足条件
，则z=6x+8y的最大值是（ ）
|
分析：先画出可行域，然后把z=6x+8y变形为直线 y=-
x+
（即斜率为-
，在y轴上的截距为
），再画出其中一条 y=-
x，最后通过平移该直线发现当这类直线过点A时其在y轴上的截距最大，则问题解决．
| 3 |
| 4 |
| z |
| 8 |
| 3 |
| 4 |
| z |
| 8 |
| 3 |
| 4 |
解答：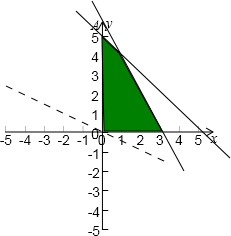
解：画出可行域
又z=6x+8y可变形为直线y=-
x+
，
所以当该直线经过点A时z取得最大值，
且解得点A的坐标为（0，5），
所以zmax=0+8×5=40．
故选B．
解：画出可行域又z=6x+8y可变形为直线y=-
| 3 |
| 4 |
| z |
| 8 |
所以当该直线经过点A时z取得最大值，
且解得点A的坐标为（0，5），
所以zmax=0+8×5=40．
故选B．
点评：本题考查画可行域及由可行域求目标函数最值问题，解题的关键是画出满足条件的区域图，属于基础题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
已知非负实数x，y满足已知非负实数x，y满足x+y=1，则
+
的最小值为（ ）
| 1 |
| x+1 |
| 4 |
| y+1 |
| A、1 | B、2 | C、3 | D、4 |