题目内容
已知非负实数x,y满足x≠y,且
≤4,则S=y-2x的最小值是
| x2+ y2 |
| x+y |
-2-2
| 10 |
-2-2
.| 10 |
分析:将已知不等式化为(x-2)2+(y-2)2≤8,结合圆的方程,得出不等式表示的平面区域,再结合线性规划问题解决.要注意分清何时取得最小值.
解答: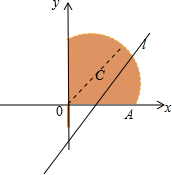 解:由已知,将不等式
解:由已知,将不等式
≤4,化为x2+y2≤4(x+y),移向配方得(x-2)2+(y-2)2≤8,表示以C(2,2)为圆心,以2
为半径的圆及其内部在第一象限的部分(除去y=x),将S=y-2x变形为y=2x+S,当直线l:y=2x+S与圆相切于第一象限时,S取得最小值,由圆的切线性质,圆心C(2,2)到l的距离等于半径长.
即
= 2
,解得S=-2-2
,(S=-2+2
舍去),
故答案为:-2-2
,
 解:由已知,将不等式
解:由已知,将不等式| x2+ y2 |
| x+y |
| 2 |
即
| |2+S| | ||
|
| 2 |
| 10 |
| 10 |
故答案为:-2-2
| 10 |
点评:本题考查了圆的标准方程,线性规划问题,将不等式转化成圆的标准方程形式是关键.易错之处是将A(4,0)作为最小值点.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知非负实数a,b满足2a+3b=10,则
+
最大值是( )
| 3b |
| 2a |
A、
| ||
B、2
| ||
| C、5 | ||
| D、10 |
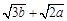 最大值是 ( )
最大值是 ( )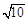 B.
B.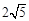 C.5 D.10
C.5 D.10 最大值是( )
最大值是( )
